正交對角拉丁方

正交對角拉丁方(orthogonal diagonal Latin squares)是一類特殊的正交拉丁方，若一個v階拉丁方的主對角線(位置(i，i)，1≤i≤v)與反對角線(位置(i，v+1-i)，1≤i≤v)均為截態，則稱之為對角拉丁方。兩個正交的v階對角拉丁方記為ODLS(v)，正交對角拉丁方曾用於構作幻方，而ODLS(v)存在的充分必要條件是v≠2，3，6，這是經許多作者的努力，由沃利斯(W.D.Wallis)等人於1990年最後完成的。

基本介紹

• 中文名：正交對角拉丁方
• 外文名：orthogonal diagonal Latin squares
• 所屬學科：數學
• 所屬問題：組合學（組合設計）
• 簡介：一類特殊的正交拉丁方

基本介紹

設X為n元集，A為X上的r×s陣列，若同行和同列都沒有重複的元素，則稱A為X上的一個r×s拉丁矩。特別地，當r=s=n時，便得到一個n階拉丁方。若集X={1，2，…，n}上的n階拉丁方A=(a_ij)滿足a_ii=i，1≤i≤n，則稱該拉丁方是冪等的。若A滿足a_ij=a_ji，1≤i≤j≤n，則稱之為對稱拉丁方。若一個n階拉丁方的n個位置分布在不同行及不同列且含不同的元素，則稱這n個位置構成該拉丁方的一個截態。若一個拉丁方的主對角線(位置(i，i)，1≤i≤n)及反對角線(位置(i，n+1-i)，1≤i≤n)均為截態，則稱之為對角拉丁方。

對角拉丁方是主對角線和反對角線均為截態的拉丁方。

若n階拉丁方A的轉置矩陣A^T(它當然還是一個n階拉丁方)恰好是A的正交侶，則稱A為一個n階自正交拉丁方。例如

與

是正交的，因此A(或A^T)就是一個4階自正交拉丁方。自正交拉丁方的存在性問題已於1974年最終解決，結論是：除去n=2，3，6不存在外，對任意正整數n存在自正交拉丁方。

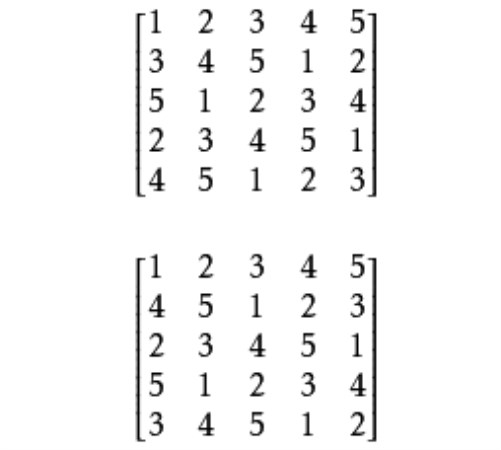
若n階拉丁方A的兩條大對角線恰是它的兩個截態，則稱A為n階對角拉丁方，兩個n階對角拉丁方若正交，則稱它們為(一對)n階正交對角拉丁方。例如

與

就是一對5階正交對角拉丁方。一對正交的對角拉丁方的存在性問題也已經解決，結論與自正交拉丁方的一樣，而三個兩兩正交的n階對角拉丁方的存在性已證明除去n=2，3，4，5，6時不存在及n=10，14，15，18，21，22，26，30，33，34，46時尚未知外對其他n值均存在。

相關研究成果

一個n階拉丁方是含n個相異元素的集X上的一個n階方陣，其每一行和每一列都是X的一個置換，n階拉丁方的一條截態是位於不同行不同列的n個位置使得其中的n個元素兩兩相異，階n的截態拉丁方的主對角線(位置{(i,i):1≤i≤n})是一條截態，階n的對角拉丁方是一個截態拉丁方，其反對角線(位置((i,n+1-i):1≤i≤n})也是一條截態。

兩個n階拉丁方稱為正交的，如果把它們迭合在一起時，第一個拉丁方的每一個記號與第二個拉丁方的每一個記號相遇一次且僅相遇一次，t個兩兩正交的n階(對角,截態)拉丁方，簡記作tPOLS(n) (PODLS(n)，POILS(n)),是t個兩兩正交的拉丁方,其每一個都是n階(對角,截態)拉丁方。為方便計我們以記號N(n)(D(n)，I(n))記兩兩正交的n階(對角，截態)拉丁方的最大個數。

t個兩兩正交的n階對角拉丁方的存在性已被許多數學工作者研究過：對於t=1，已經證明對所有大於3的正整數n存在n階對角拉丁方；對於t= 2，已經證明對所有大於6的正整數n存在階為n的一對正交對角拉丁方。對於t≥3，已知的結果較少。利用成對平衡設計的方法，Wallis與朱烈在給出了一些界，即當n≥447時D(n)≥3，當n≥511時D(n)≥4，以及當n≥2724時D(n)≥5，漸近地中已證明當n→∞時D(n)→∞。後來利用特異直積的方法，朱烈進一步證明除28個可能的例外，當n≥7時存在三個兩兩正交的n階對角拉丁方，其中118是最大可能的例外值；Wallis和朱烈進一步證明除18個可能的例外，當n≥7為奇數時存在四個兩兩正交的n階對角拉丁方，其中291是最大可能的例外值。

朱烈

朱烈是江蘇蘇州人，現任蘇州大學教授，兼加拿大《組合學》雜誌編委。論著有《尤拉猜想的簡短證明》、《具齊位子方的正交拉丁方的存在性》、《三個兩兩正交對角拉丁方》、《具相等大小洞的相互正交拉丁方的存在性》等。

朱烈對於兩兩正交的v階對角拉丁方的最大個數作了一系列研究，利用他本人及其他學者的結果，他最後證明了，當v≥7時，除了28個可能的例外值，存在三個兩兩正交的v階對角拉丁方。用d_r記符合下述條件的最小正整數：當v>d_r時，存在r個兩兩正交的v階對角拉丁方。已知d₂<10。 W.D.Wallis和朱烈證明了d₃≤446,d₄≤510,d₅≤2723，d₆≤6277。