基本介紹
- 中文名:不完全拉丁方設計
- 外文名:Incomplete Latin Squares
- 所屬學科:數學(統計學)
- 別名:堯敦方設計、YOUDEN方設計等
基本介紹,套用條件,不完全拉丁方設計的特點,
基本介紹
不完全拉丁方設計類似於平衡不完全隨機區組設計,在3因素的拉丁方設計中,當處理水平數固定的情況下,如果其他兩個區組因素中有一個水平數小於處理水平數,此時不滿足拉丁方設計中水平數必須相等的條件,可以考慮採用不完全拉丁方設計。不完全拉丁方設計雖然稱為Youden square,但它實際上已經不是square了,因為行列數並不相等。不完全拉丁方設計亦稱尤登方設計,是用尤登方安排的一種部分實施試驗設計。用於由於客觀條件的限制無法完整地用拉丁方安排試驗的情形,或者用於由拉丁方設計的試驗結果有丟失數據的情形,其結果的分析與拉廠方設計類似。
通常所說的不完全拉丁方設計(也稱“堯敦方設計”)的形式是列區組的水平數k小於行區組水平數b(等同於處理水平數t)的設計,該設計共bc個受試對象。如果僅看列區組,不考慮行區組,堯敦方設計是一個完全隨機區組設計;如果僅看行區組,不考慮列區組,堯敦方設計則是一個平衡不完全隨機區組設計,圖1給出了3×2、4×3兩種不完全拉丁方設計的形式。
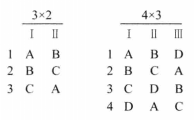 圖1 幾種常見不完全拉丁方設計
圖1 幾種常見不完全拉丁方設計圖1是不完整拉丁方設計的一個樣式例子。這是一個具有7種水平,7行3列的設計,重要的是將不同水平被分配到行列的順序,注意除具有平衡不完全區組設計的特點外,YOUDEN方設計中,每一種處理在每列中恰好出現一次。處理數t等於區組數b。
區組 | 列 | ||
1 | 2 | 3 | |
1 | T1 | T2 | T3 |
2 | T2 | T3 | T4 |
3 | T3 | T4 | T5 |
4 | T4 | T5 | T6 |
5 | T5 | T6 | T7 |
6 | T6 | T7 | T1 |
7 | T7 | T1 | T2 |
YOUDEN方設計有些可以通過平衡不完全設計得到,有些可以通過設計完全拉丁方法後略去某一行或列而獲得。
YOUDEN方設計用於處理因素水平數較多的實驗,有多種類型的處理因素。由於列數少於處理數,所以每一行僅有部分處理方式被套用。有時一些雙向控制變數或雙向分類的實驗需要這種設計。
套用條件
當客觀條件限制不能用拉丁方設計時,可用拉丁方的一部分來安排試驗,稱為不完全拉丁方(或Youden方、堯敦方)設計。或雖用了拉丁方設計,但某一行或某一列缺失數據較多,又無法補救時,可根據情況作不完全拉丁方資料處理。
不完全拉丁方設計的特點
不完全拉丁方設計的主要特點為:
(1)處理水平數t等同於行數b,處理水平重複數r等同於列數k。處理水平每列出現1次,每行最多出現1次。
(2)每一對處理在行區組中出現的次數 ,是一自然數。如3×2堯敦方設計中,
,是一自然數。如3×2堯敦方設計中, ,每一對處理(AB、AC、BC)在行區組中各出現1次;4×3堯敦方設計中,
,每一對處理(AB、AC、BC)在行區組中各出現1次;4×3堯敦方設計中, ,每一對處理(AB、AC、AD、,BC、BD、CD)在行區組中各出現2次。
,每一對處理(AB、AC、AD、,BC、BD、CD)在行區組中各出現2次。




