基本介紹
- 中文名:不完全拉丁方設計
- 外文名:Incomplete Latin Squares
- 所屬學科:數學(統計學)
- 別名:堯敦方設計、YOUDEN方設計等
基本介紹
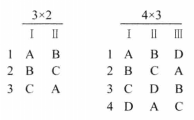 圖1 幾種常見不完全拉丁方設計
圖1 幾種常見不完全拉丁方設計區組 | 列 | ||
1 | 2 | 3 | |
1 | T1 | T2 | T3 |
2 | T2 | T3 | T4 |
3 | T3 | T4 | T5 |
4 | T4 | T5 | T6 |
5 | T5 | T6 | T7 |
6 | T6 | T7 | T1 |
7 | T7 | T1 | T2 |
套用條件
不完全拉丁方設計的特點



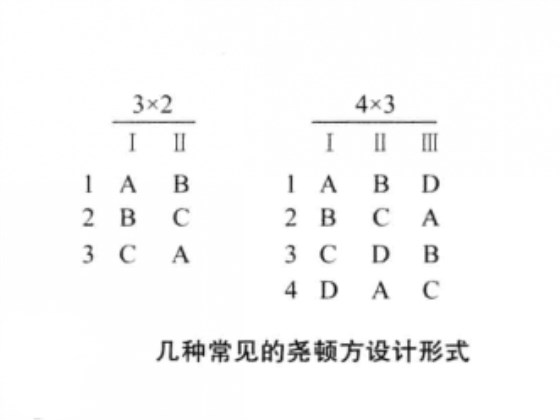
 圖1 幾種常見不完全拉丁方設計
圖1 幾種常見不完全拉丁方設計區組 | 列 | ||
1 | 2 | 3 | |
1 | T1 | T2 | T3 |
2 | T2 | T3 | T4 |
3 | T3 | T4 | T5 |
4 | T4 | T5 | T6 |
5 | T5 | T6 | T7 |
6 | T6 | T7 | T1 |
7 | T7 | T1 | T2 |



在拉丁方設計中,三個因素要求相同的水平數,即行,列,字母數均相同,但在具體實踐中可能其中一個因素水平數較少,這時就不能採用完整的拉丁方設計,則可用不完全拉丁...
拉丁方設計(Latin square design)是以表格的形式被概念化,其中行和列代表兩個外部變數中的區組,然後將自變數的級別分配到表中各單元中。簡單的說就是某一變數在...
部分平衡不完全區組設計分類 編輯 按結合方案的類型,具有兩個結合類的PBIBD設計可分為可分組PBIBD設計、三角形設計、拉丁方型設計等,利用有限域上向量空間以及利用...
拉丁方試驗設計,是指在統計上能控制兩個不相互作用的外部變數,每個外部變數或分區變數被劃分為一個相等數目的級別且自變數也同樣被分為相同數目的級別,即拉丁方排列...
正交拉丁方設計是使用正交拉丁方安排的一種試驗方案,當存在m個相互正交的n階拉丁方時,用拉丁方的行和列分別表示兩個因素的n個水平,用這m個拉丁方的記號分別表示...
用完全的平衡方法或拉丁方方法,可克服實驗順序帶來的缺點。如在視、聽覺的反應...被試內設計是指每個或每組被試接受所有自變數水平的實驗處理的真實驗設計。其...
矩形格子設計是在拉丁方設計的基礎上進行的,先找一個(p+1)×(p+1)的拉丁方,行與列要進行隨機化處理,不考慮主對角線,然後可以按行劃分不完全區組,亦可以按...
4.4完全隨機區組試驗設計的評價 4.4.1優點 4.4.2缺點 習題 第5章拉丁方試驗設計 5.1拉丁方簡介 5.2拉丁方設計的原理 5.3拉丁方設計的試驗布置 5...
如果只有A、B兩種序列,最常用的抵消方法是ABBA的安排,如果對幾組被試給予兩種以上的處理,最常用的抵消方法是拉丁方設計。中文名 平衡抵消設計;平衡抵消法 外文名...
如ABBA設計、拉丁方設計等。與隨機化區組設計對應的是完全隨機化設計,又叫組間設計、獨立組設計。實驗中每個被試只接受一個處理,不存在處理間的污染問題,但無法...
以完全隨機化設計、隨機化區組設計和拉丁方設計為基礎。有完全隨機化析因設計、隨機化區組析因設計、裂區析因設計、混雜析因設計、部分析因設計等種類。 [1] ...
1 概述 2 區組設計 3 拉丁方 4 不完全區組設計 5 不完全區組分類 6 析因設計 7 部分實施法 8 正交表 實驗設計法概述 編輯 這...
用隨機區組或拉丁方設計在同一區組內已不具有土壤條件同質性,因而根據“局部控制”原則改用不完全區組設計以代替完全區組設計,使不完全區組之間的差異可從試驗...
第四節隨機區組設計的統計分析及SAS實現 一、完全隨機區組設計的統計分析 二、平衡不完全區組設計的統計分析 第五節案例辨析 第五章拉丁方設計與分析 第...
第4章 比較多個總體:隨機區組和拉丁方4.1 在一個完全隨機設計中比較k個處理4.2 隨機區組設計4.3 裂區試驗初步及其與隨機區組的關係...
尤登方(Youden square)亦稱尤登設計。如果從一個拉丁方中划去至少一列(或行)並將行(或列)因子看作區組因子,仍然成為一個平衡不完全區設計的話,則稱這個不...
