基本介紹
- 中文名:扭結
- 外文名:Knot theory
- 類型:幾何直觀對象
- 所屬:數學
- 鏈環:若干個扭結套在一起
歷史
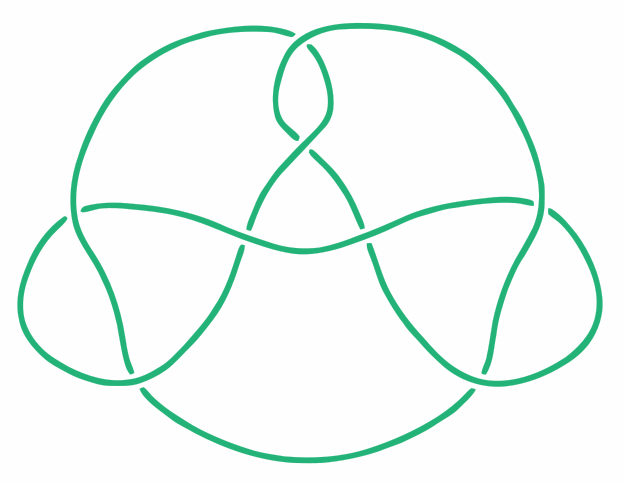 圖1.較為複雜的紐結
圖1.較為複雜的紐結- 在兩個方向扭曲和解開。
- 將一條鏈完全移到另一條鏈上。
- 完全在一個十字路口上或下面移動一根線。
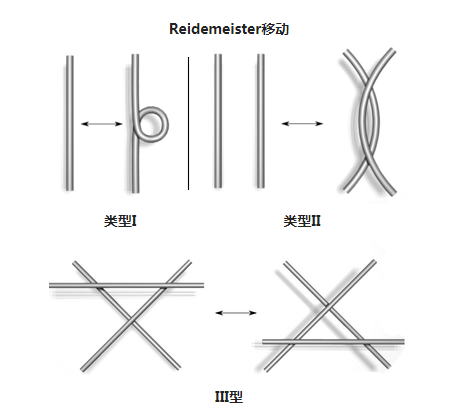 圖2.Reidemeister 移動
圖2.Reidemeister 移動紐結連通和
 圖3.用三維模型展示扭結
圖3.用三維模型展示扭結
 圖1.較為複雜的紐結
圖1.較為複雜的紐結 圖2.Reidemeister 移動
圖2.Reidemeister 移動 圖3.用三維模型展示扭結
圖3.用三維模型展示扭結扭結編輯 鎖定 本詞條由“科普中國”百科科學詞條編寫與套用工作項目 審核。紐結理論是拓撲學的一個分支,研究紐結的拓撲學特性。在拓撲學中,結理論是數學結的研究...
歐氏空間R3中的簡單閉曲線稱為扭結(knot)。由有限條直線所組成的扭結稱為多邊形扭結。設K1和K2是扭結,如果存在同胚h: R3→R3,使得h(K1)=K2,則稱它們是等價的...
三葉扭結是由莫比烏斯帶演變而成的。是由一條三稜柱帶經過三次盤繞,將其中的一端旋轉120゜後首尾相接,構成三面連通的單側單邊的三葉扭結造型。...
扭結包裝為最傳統的糖果包裝方式之一,它和枕包、摺疊式包裝並稱糖果包裝三大包裝方式。扭結包裝的主要材質已由原來的PVC轉換成環保型材料PET扭結膜。...
扭結式縫襪頭,又稱羅斯特縫襪頭。一種在圓襪機上用扭結的方式封閉襪頭的工藝。採用此工藝的“單針筒襪機”通常備有“哈夫針”裝置。編織襪頭開始,哈夫針伸出...
中文名 環面扭結 外文名 torus knot 紐結理論中,一個環結是一種特殊的結,在R3中的一個解開這個圓環面。同樣,一個圓環鏈是一個連結,它位於一個圓環面的表面...
內容簡介“彗尾扭結”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。 中文...
扭結軟糖是澳門特色小吃之一,已經有百年的歷史,已成為祖國大陸、港澳台、世界各地唐人街、歐美等國家地區的特色產品。...
扭結紗在織物中看起來就好象是細小的搓捻。詞條標籤: 工業產品 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:3次歷史版本 最近更新: 創建者:董董瑲...
肉鬆扭結包是一道美食,由優質小麥粉,酵母,糖等原料製作而成。...... 肉鬆扭結包是一道美食,由優質小麥粉,酵母,糖等原料製作而成。中文名 肉鬆扭結包 主要食材...
扭結小麵包編輯 鎖定 討論999 一樣的麵包方子,不一樣的麵包造型。這款麵包沒有放黃油或是植物油,做了這么長時間的麵包,經過比對,我覺得放油與不放油,麵包在...
扭結試驗儀是一款適用於導體截面積在1.5mm2及以下的二芯和三芯護套軟線的儀器。...... 扭結試驗儀是一款適用於導體截面積在1.5mm2及以下的二芯和三芯護套軟...
氣動定量扭結灌腸機,採用先進技術運用氣動、光電控制原理,可連續自動定量灌裝扭結,適合灌裝各種、火腿類產品,適合天然腸衣、膠原、煙燻腸衣。此機體積小,投入低,適用...
高維扭結(high dimensional knot)扭結概念在一般高維流形的推廣.若M為n維流形,則s -z在M的一個嵌入,當n}3時稱為一個高維扭結.類似地,若S1,S2,S3為無交...
蜂蜜扭結包,是一道美食,主料為高粉250克,配以蜂蜜、雞蛋、黃油等材料,經烤制而成,味道甜美。...
扭結式裹包機 twist wrapping machine 用撓性包裝材料裹包產品,將末端伸出的裹包材料扭結封閉的機器 ...
雙色扭結酥是一道美食,由低粉等主料和相關輔料製作而成。...... 雙色扭結酥是一道美食,由低粉等主料和相關輔料製作而成。中文名 雙色扭結酥 主要原料 低粉...
電線扭結試驗機適用於測試電線耐扭結性能。MK-810電線扭結試驗機符合HD22.3-1997、IEC60227、GB5013、5023等試驗標準。...
參考資料 1. 扭結餐包 .下廚房 作者:子-迪 [引用日期2014-06-08] 詞條標籤: 生活 圖集 扭結餐包圖冊 V百科往期回顧 權威合作編輯 下廚房 唯有美食與愛...
胡蘿蔔扭結餐包是一道美食,主要製作材料有小麥麵粉、胡蘿蔔、水等。...... 胡蘿蔔扭結餐包是一道美食,主要製作材料有小麥麵粉、胡蘿蔔、水等。中文名 胡蘿蔔扭結...
《雙向拉伸聚苯乙烯扭結薄膜(GB/T 26191-2010)》的標準按照GB/T 1.1—2009給出的規則起草。請注意本檔案的某些內容可能涉及專利。本檔案的發布機構不承擔識別...
Bretzel,也有人稱它為蝴蝶脆餅,來源於德國或法國阿爾薩斯。它通常是蝴蝶形的,用小麥粉製成,口味是鹹的。也有的翻譯成德國結,迷你餅乾圈,扭結餅,椒鹽卷餅等等。...
