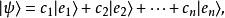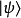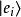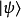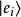基本介紹
- 中文名:態向量
- 外文名:State vector
- 領域:量子力學
簡介,量子態,內積空間,
簡介
在量子力學里,一個量子系統的量子態可以抽象地用態矢量來表示。態矢量存在於內積空間。定義內積空間為增添了一個額外的內積結構的矢量空間。態矢量滿足矢量空間所有的公理。態矢量是一種特殊的矢量,它也允許內積的運算。態矢量的范度是1,是一個單位矢量。標記量子態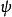 的態矢量為
的態矢量為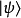 。
。
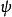
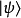
換一種方法表達:
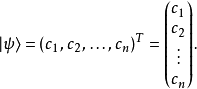
在狄拉克標記方法裡,態矢量 稱為右矢。對應的左矢為
稱為右矢。對應的左矢為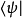 ,是右矢的厄米共軛,用方程表達為
,是右矢的厄米共軛,用方程表達為

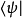
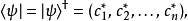
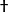
設定兩個態矢量 ,
,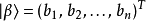 。定義
。定義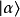 內積
內積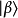 為
為

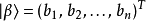
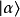
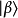

這內積的結果是一個複數。
量子態
在量子力學里,量子態(英語:quantum state)指的是量子系統的狀態。態矢量可以用來抽像地表示量子態。採用狄拉克標記,態矢量表示為右矢 ;其中,在符號內部的希臘字母
;其中,在符號內部的希臘字母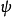 可以是任何符號,字母,數字,或單字。例如,在計算氫原子能譜時,能級與主量子數
可以是任何符號,字母,數字,或單字。例如,在計算氫原子能譜時,能級與主量子數 有關,所以,每個量子態的態矢量可以表示為
有關,所以,每個量子態的態矢量可以表示為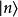 。
。


一般而言,量子態可以是純態或混合態。上述案例是純態。混合態是由很多純態組成的機率混合。不同的組合可能會組成同樣的混合態。當量子態是混合態時,可以用密度矩陣做數學描述,這密度矩陣實際給出的是機率,不是密度。純態也可以用密度矩陣表示。
內積空間
內積空間是數學中的線性代數里的基本概念,是增添了一個額外的結構的向量空間。這個額外的結構叫做內積或標量積。內積將一對向量與一個標量連線起來,允許我們嚴格地談論向量的“夾角”和“長度”,並進一步談論向量的正交性。內積空間由歐幾里得空間抽象而來(內積是點積的抽象),這是泛函分析討論的課題。
在早期的著作中,內積空間被稱作酉空間,但這個詞現在已經被淘汰了。在將內積空間稱為酉空間的著作中,“內積空間”常指任意維(可數或不可數)的歐幾里德空間。