基本介紹
公式含義



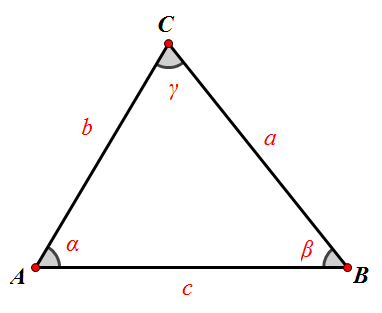
餘弦定理表達式1








驗證推導
《欽定四庫全書》上的證明
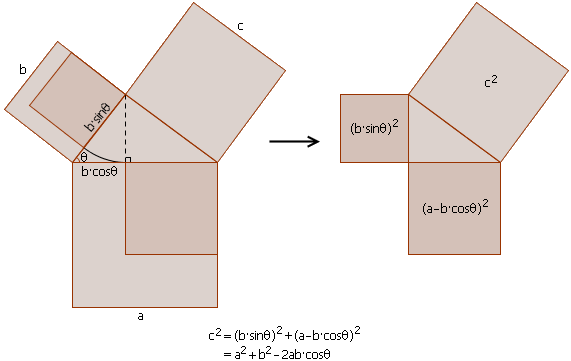
無字證明
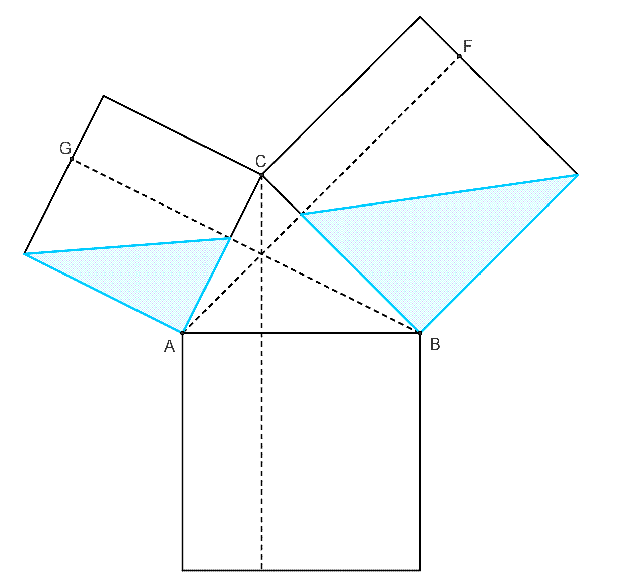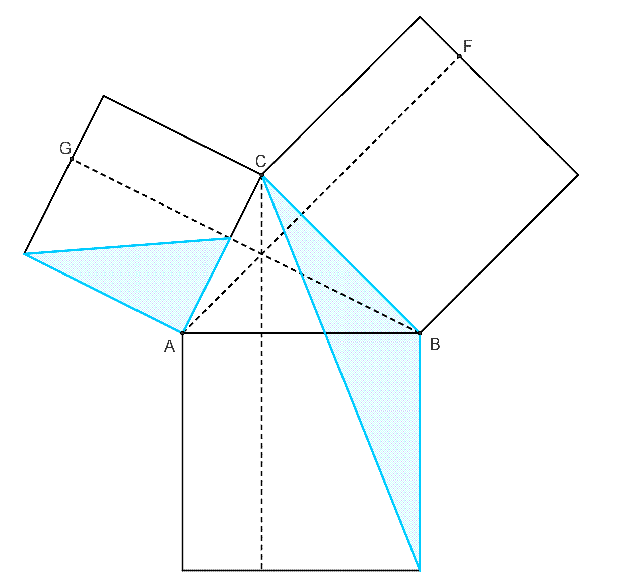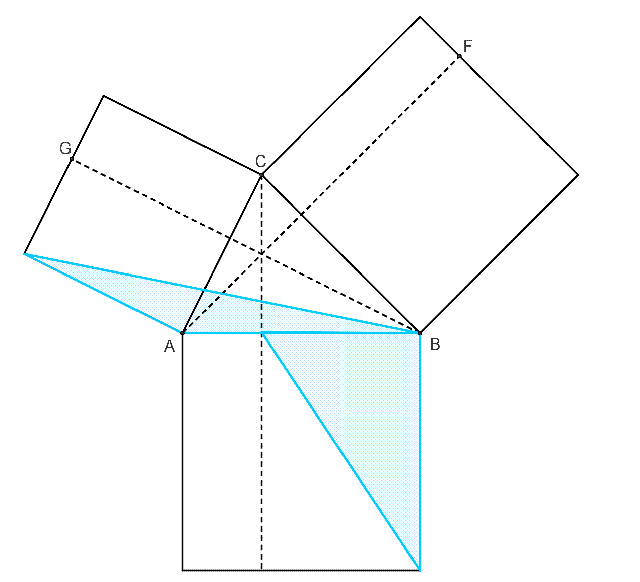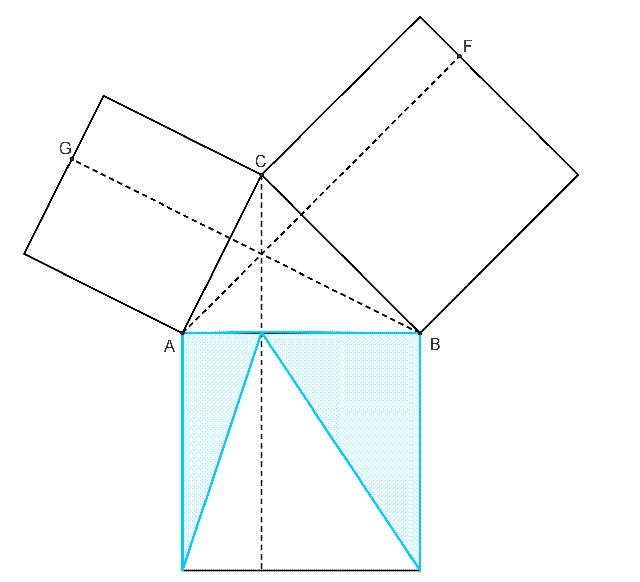
平面幾何法證明一
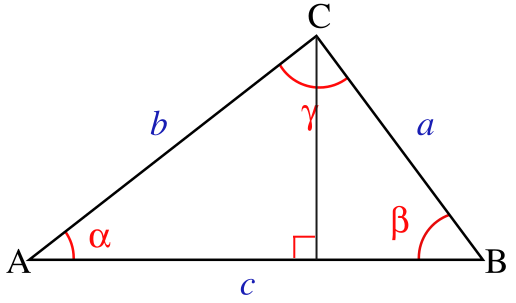




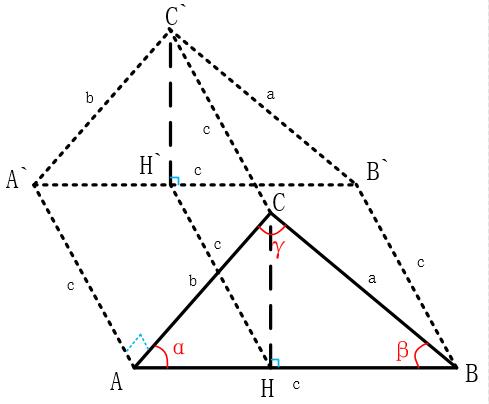





平面幾何法證明二
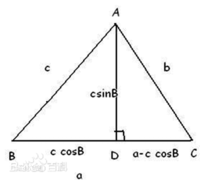
利用正弦定理證法
平面向量證法
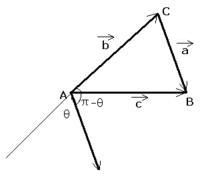
定理套用
- 當已知三角形的三邊,可以由余弦定理得到三角形的三個內角。
- 當已知三角形的三邊,可以由余弦定理得到三角形的面積。
求邊



求角



求面積

判定定理
判定定理一 兩根判別法
判定定理二 角邊判別法
套用例題
例如
再如


廣勾股定理一般指本詞條




































勾股定理是餘弦定理中的一個特例。推導 趙爽弦圖 《周髀算經》中,趙爽描述此圖:“勾股各自乘,並之為玄實。開方除之,即玄。案玄圖有可以勾股相乘為朱實二,倍之為朱實四。以勾股之差自相乘為中黃實。加差實亦成玄實。以差實...
勾股定理是人類早期發現並證明的重要數學定理之一。據《周髀算經》中記述,公元前一千多年周公與商高論數的對話中,商高就以三四五3個特定數為例詳細解釋了勾股定理要素,其一,“以為句廣三,股修四,徑隅五”。其二,“既方其外,...
勾股定理在西方被稱為Pythagoras定理,它以公元前6世紀希臘哲學家和數學家的名字命名。可以有理由認為他是數學中最重要的基本定理之一,因為他的推論和推廣有著廣泛的引用。雖然這樣稱呼,他也是古代文明中最古老的定理之一,實際上比...
勾股定理是數學中最重要的定理之一。也許在數學中還找不到這樣一個定理,其證明方法之多能夠超過勾股定理。它有四百多種證明。盧米斯(Loomis)在他的《畢達哥拉斯定理》一書的第二版中,收集了這個定理的370種證明並對它們進行了分類...
《勾股定理》是科學出版社出版的圖書,作者是(英)格倫(W.H.Glenn),(英)詹森(D.A.Johnson)。 內容簡介 這本小冊子是《自修數學》小叢書中的一本.勾股定理或商高定理在西方稱為畢達哥拉斯定理.書中以通俗易懂的語言和生動有...
餘弦定理是描述三角形中三邊長度與一個角的餘弦值關係的數學定理,是勾股定理在一般三角形情形下的推廣,勾股定理是餘弦定理的特例。餘弦定理是揭示三角形邊角關係的重要定理,直接運用它可解決一類已知三角形兩邊及夾角求第三邊或者是已知...
一般認為《周髀算經》成書於公元前1世紀,可見我國至少在2100年前就發現了勾股定理。《勾股舉隅》《勾股舉隅》為梅文鼎研究中國傳統勾股算術的著作,全書一卷,其中的主要成就,是對勾股定理的證明和對勾股算術算法的推廣。書中首列“和較...
高斯—馬爾可夫定理 更比定理 谷山-志村定理 哥德爾完備性定理 哥德爾不完備定理 割線定理 廣義正交定理 古爾丁定理(古爾亭定理)高斯散度定理 古斯塔夫森定律 共軛復根定理 高斯-盧卡斯定理 哥德巴赫-歐拉定理 勾股定理 格爾豐德-施奈德定理...
“勾股模型”是《夸克模型》之後,由中國閃爍軟體公司“耗散的空虛”領導的專利開發小組對基本粒子的一種表述模型。圖片圖示 勾股模型圖示 簡述 《勾股模型》在有理數範圍內表述了基本粒子的結構和組成,套用勾股定理理論描述了球體在三維...
在《周髀》和《九章》中,都已經明確給出了勾股定理的一般形式:勾2+股2=弦2。雖然原證不傳,但是據《勾股說》以及《劉注》,都依出入相補原理證明,並且有遺留到可以用來作證的趙爽殘圖,這幾方面互相參照,原證應該大致如下:勾...
雖夫圓穹之象猶曰可度,又況泰山之高與江海之廣哉。”。這段論述,是勾股定理在古代中國用於立桿測影的佐證之一。因此,歷代中國數學家對勾股理論非常重視,傾注大量心血進行研究,成果斐然,以東漢末期趙爽勾股弦圖(即:勾股圓方圖)...
在《周髀算經》中記載的榮方和陳子的問答中,談到了由勾股求弦的一般方法“勾股各自乘,並而開方除之”。可見古代勞動人民已將勾股定理運用於生產實踐之中。一般認為《周髀算經》成書於公元前1世紀,可見我國至少在2100年前就發現了...
《周髀算經》原名《周髀》,算經的十書之一,是古老的天文學和數學著作,主要闡明當時的蓋天說和四分曆法。唐初規定它為國子監明算科的教材之一,故改名《周髀算經》。《周髀算經》證明了勾股定理。《周髀算經》採用最簡便可行的方法...
“勾三股四弦五”是勾股定理的一個特別的例子,由西周初年的商高提出。但只是適應於直角三角形,(3角度數為36.8698976 °,53.1301024°,90°。)中國古代稱短的直角邊為勾,長的直角邊為股,斜邊為弦。據我國西漢時期算書《...
和較術亦稱勾股和較術。和較術亦稱勾股和較術.中國古算法.指中國古代勾股定理套用的一個重要組成部分.“較”在中國古代數學中是“差”的意思.在勾股形中,設其勾、股、弦分別為a,b,c,且有a a+b, a+c, b+c, b-a, c-...
