平行四邊形定則

平行四邊形定則是數學科的一個定律。兩個向量合成時，以表示這兩個向量的線段為鄰邊作平行四邊形，這個平行四邊形的對角線就表示合向量的大小和方向，這就叫做平行四邊形定則（Parallelogram law）。

基本介紹

• 中文名：平行四邊形定則
• 外文名：parallelogram law
• 別稱：平行四邊形法則
• 表達式：F2=F12+F22+2F1F2Cosθ
• 提出者：皮耶利·瓦里翁
• 提出時間：1726年
• 套用學科：數學、物理
• 適用領域範圍：物理
• 適用領域範圍：物理力學

發展簡史

1586年，荷蘭的斯蒂文在《靜力學基礎》一書中最早提出力的分解與合成原理，並把這一原理（沒有明確表達出）套用到兩繩懸一重物、一繩在三處掛不同重物等場景中，解決了許多複雜問題。

1687年，牛頓在《自然哲學的數學原理》的“物體的運動”的推論1、2中分別寫到：“一個物體，同時受到兩個力的作用，就將沿平行四邊形的對角線運動，所用的時間和它分開受到這兩個力的作用而沿兩邊運動的時間相同”。牛頓憑藉敏銳的直覺，推斷出了運動和力的分解與合成所遵循的定則，但未作進一步的證明。

幾乎與此同時，法國皮耶利·瓦里翁向巴黎科學院提交了由他獨立得出的諸力合成的平行四邊形定則的報告，但沒有表述清楚。1725年，瓦里翁在《新力學或靜力學》一書中用力的合成與分解原理解決了各種具體靜力學問題，並初步提出了“力矩”概念，找出了力的平行四邊形原理與力矩的關係。他還把力的平行四邊形原理推廣到運動學的速度中去，認為靜力學只是動力學的特例。

1726年，約翰·伯努利在寫給瓦里翁的信中提出力的平行四邊形原理可以用於靜力學。他用虛功原理分析在一個力學系統中力矩做功的問題，指出在任何力的平衡的情況下，無論這些力是直接地或是間接的用來支持相互平衡。丹尼爾·伯努利則在《力學原理的研究及力的分解與合成證明》一文中對瓦里翁提出兩點質疑：①力與速度在運用合成與分解時不應成正比；②在各力的作用下物體的運動是不是具有獨立性。

此後，法國的潘索也對平行四邊形定則進行了數學證明並首先引入“剛體”、“力偶”等概念，進一步將靜力學用於剛體及機器結構的分析上。直到十九世紀乃至二十世紀初，包括拉普拉斯、茹可夫斯基等眾多力學家在內，都花了許多時間來對此進行爭論。

如同慣性定律一樣，這是一條永遠無法用實驗完美證明的定則。只是隨著矢量及其所遵循的運算定則的確立，力、位移、速度等被納入力的矢量體系，以及運動的獨立性、力的獨立作用原理和物體在摩擦力下運動的動力機制被揭示，人們才從邏輯上接受了這一定則。

數學推導

平行四邊形定則，證明例圖。

F^2=CD^2+AC^2

=(F1Sinθ)^2+(F2+F1Cosθ)^2

=(F1Sinθ)^2+F2^2+2F1F2Cosθ+(F1Cosθ)^2

=F2^2+2F1F2Cosθ+F1^2

∴F=√F2^2+2F1F2Cosθ+F1^2

實驗驗證

實驗目的

驗證互成角度的兩個力合成時的平行四邊形定則。

實驗方法

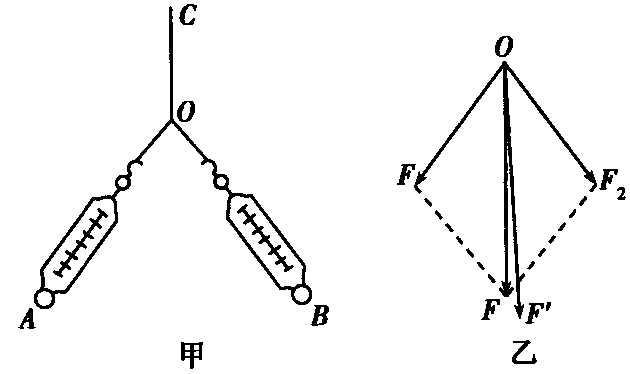
一、等效法

兩個分力共同作用於一個物體的同一點，使物體產生一定的形變或加速度。然後用一個力單獨作用於兩分力作用時的作用點上，調節該力的大小和方向，使受力物體產生與兩分力共同作用時相同的形變或加速度。由於加速度的測量比較複雜，常採用分力與合力對受力物體的相同形變，實現兩分力的共同作用與合力單獨作用等效。這時，與兩分力共同作用等效的一個力就代表兩分力的合力。

一般選橡皮筋為受力物體，將橡皮筋一端固定，用兩個互成角度的力F₁、F₂同時拉橡皮筋的另一端，使其產生一定的伸長。然後用一個力F單獨拉橡皮筋，使其產生與兩拉力共同作用時相同的伸長，則F與兩分力的合力相同。F就是測量出的合力。然後再運用平行四邊形定則求出F₁、F₂的合力。比較F與F₁、F₂的合力，看兩者大小是否相等、方向是否相同。

本實驗的成敗，關鍵是等效與誤差的控制。實現等效，就是保證橡皮筋兩次的伸長量相等，要求兩次將橡皮筋的末端拉至同一位置。控制誤差，要做到：

（1）儘量選相同的彈簧測力計。可將兩測力計鉤好對拉，選讀數始終相同的一對；

（2）測力計與固定橡皮筋的板面平行，讀數時，視線要與測力計刻度板正對；

（3）在不超過彈性限度的條件下，儘可能使拉力大一些；

（4）用力的圖示法依據平行四邊形定則畫圖求合力時，標度的選擇應儘量使圖畫得大一些，畫圖要嚴格使用作圖工具；

（5）在同一次實驗中，橡皮筋拉長後的結點位置一定要相同。

二、平衡法

三個恆力同時作用於物體的同一點，當受力物體處於靜止狀態或勻速直線運動狀態時，這三個力平衡，其中任意兩個力的合力與第三個力大小相等，方向相反。若以任意兩個力作為分力，則第三個力的大小代表前兩個力的合力大小，第三個力的反方向代表合力的方向。

實驗中，一般是將三個輕繩套一端結在一起，以結點作為受力物體。然後在其中的一個繩套掛上重物，用兩個彈簧測力計在豎直平面內沿兩個互成角度的方向分別拉另外兩個繩套，當重物靜止時，三力平衡。為方便實驗及測量，通常使受力質點保持靜止狀態，實現三個力的平衡。

本實驗關鍵是控制受力質點處於靜止狀態。減小誤差的措施與“等效法”是相同。

定律解釋

標量之間的運算只有一個要求，那就是單位要一致， 但是，矢量相加就要用特別的方法，因為被加的量既有一定數值，又有一定的方向，相加時兩者要同時考慮。在力學中經常遇到的矢量有位移、力、速度、加速度、動量、衝量、力矩、角速度和角動量等。
矢量的加法有兩種：其一即所謂三角形法則；另一方法即平行四邊形法則，它們本質是一樣的。若用三角形法則求總位移似乎直觀些，而用平行四邊形法則求力的合成好像更便於理解。
應該指出的是：合力表示的作用效果與 各個分力的共同作用效果是一樣的。因此可以用 代替“和”的共同作用，但絕不能把 當成作用在物體上的第三個力。在分析物體受力情況時，不能同時考慮合力與分力對物體的作用。有的人認為：“合力總比分力大”。我們可利用求合力的平行四邊形法則，通過作圖可看到，合力的大小是隨兩分力夾角而變化的，絕不能說“合力一定要比分力大”。

套用

一個矢量，只要遵守平行四邊形法則，可以分解為兩個，或無窮個。但是矢量的合成不同，兩個矢量只能合成為一個矢量。

套用舉例：力的合成和分解、

電場的疊加：

如果場源電荷不止一個點電荷，則根據電荷相互作用力的疊加可知，電場中各點的場強為各點電荷單獨在該點產生的場強的矢量和，這就是場強的疊加(Superposition of Electric Field).電場的疊加同樣滿足平行四邊形法則。

定律影響

平行四邊形定則方法被引進到分析和解析幾何中來，並逐步完善，成為了一套優良的數學工具。