關於三維流形的一個重要猜想。它指的是一個三維流形能分割成具有八種標準幾何結構之一的子流形。 它是二維曲面單值化定理在三維流形上的一個類似。
基本介紹
- 中文名:幾何化猜想
- 外文名:Geometrization conjecture
- 提出者:威廉.瑟斯頓
- 提出時間:1982
- 套用學科:數學
- 適用領域範圍:低維拓撲
簡介
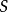


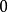
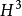
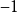


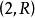
關於三維流形的一個重要猜想。它指的是一個三維流形能分割成具有八種標準幾何結構之一的子流形。 它是二維曲面單值化定理在三維流形上的一個類似。
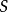


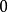
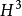
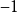


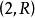
關於三維流形的一個重要猜想。它指的是一個三維流形能分割成具有八種標準幾何結構之一的子流形。 它是二維曲面單值化定理在三維流形上的一個類似。...
威廉·瑟斯頓在1970年代末提出的幾何化猜想提供了在低維中幾何與拓撲之間的關係的理論基礎。瑟斯頓使用過去在數學中只是很弱地互相關聯的分支的不同技術解決了Haken...
數學猜想有的被驗證為正確的(如費馬猜想、卡塔蘭猜想、龐加萊猜想等),並成為...數學猜想各種猜想 編輯 成立的(定理)幾何化猜想四色定理( 2008理論證明完成)龐...
在2002年11月和2003年7月之間,俄羅斯的數學家格里戈里·佩雷爾曼在發表了三篇論文預印本,並聲稱證明了幾何化猜想。在佩雷爾曼之後,先後有2組研究者發表論文補全...
橢圓化猜想是更廣的Thurston幾何化猜測的一個特例(對應球面幾何情形)。Smale,Freedman,Thurston都是由於以上這些所提到的工作,獲得了菲爾茲獎。可見這個問題的重要。...
這些文章似乎說明佩雷爾曼證明了幾何化猜想,這個猜想的一個特殊情況就是龐加萊猜想。許多人認為,法國數學家亨利·龐加萊於1904年提出的龐加萊猜想是拓撲學最著名...
數學難題可以是指那些歷經長時間而仍未有解答/完全解答的數學問題。古今以來,一些特意提出的數學難題有:平面幾何三大難題、希爾伯特的23個問題、世界三大數學猜想、...
威廉·瑟斯頓幾何化猜想 編輯 美國康奈爾大學的數學家威廉·瑟斯頓(William Thurston),他說:“數學是真正的人類思維,它涉及人類如何能有效地思考,這就是為什麼好奇心...
這些文章似乎說明佩雷爾曼證明了幾何化猜想,這個猜想的一個特殊情況就是龐加萊猜想。許多人認為,法國數學家昂利·龐加萊於1904年提出的龐加萊猜想是拓撲學最著名...
三維的幾何化猜想(現為定理)表示,每個三維流形都可被分解成數個質流形,而每個質流形都會是八種幾何的其中一種。二維拓撲可被視為具單一變數的復幾何(在黎曼...
關於三維流形的內容有三維流形的素分解,JSJ分解,Heegaard分解,Dehn 手術描述,分支覆蓋描述,Poincare 猜想,Thurston 幾何化猜想。其中兩個猜想都被俄羅斯數學家 ...
三維流形的研究中,瑟斯頓的工作非常重要,他發現雙曲幾何在三維流形的研究中起突出的作用。瑟斯頓提出的幾何化猜想是比龐加萊三維球面猜想更廣泛的猜想,後與龐加萊...
