綜述
《同調論》是現代數學的重要基礎課程,也是套用數學的基本研究對象之一,它偏重於用代數方法來 研究
拓撲學問題,即用代數作為工具研究拓撲空間的自身結構及空間圖形在連續形變下保持不變的性質。 《同調論》採用了極為有力的表述形式及高度抽 象的觀點、方法,使他的理論顯得十分簡捷而具有高度的概括力,以致它的理論廣泛地套用到現代數學的各個分支。《同調論》不僅在微分幾何、複變函數、代數幾何、抽象代數、代數數論、微分方程、對策論等其他許多數學分支中有著廣泛的套用。而且在自然科學和其它工程技術領域的許多學科諸如:電路網路、理論物理、計算機、電子通訊、現代控制理論乃至原子核構造理論等學科都具有廣泛的套用。已成為現代數學及現代技術領域中不可替代的基礎工具之一,也是非數學類眾多領域的本科生及研究生必修的數學基礎課程。
 同調論
同調論 同調論
同調論代數拓撲學中的一個主要組成部分,研究與同調概念有關的課題。
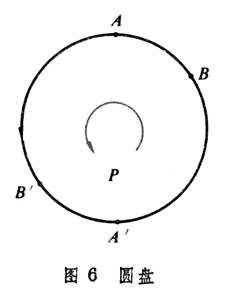
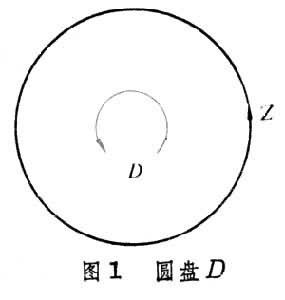
考慮帶有方向的曲面(塊)與曲線(段),如圖1、圖2中的圓盤均由旋轉箭頭定向。圓周Z與Z┡是比
D與
D┡低一維的圖形,作為曲線,它們各按所標的箭頭定向。規定
D的邊緣為Z,記作嬠
D=Z;對於
D┡,則應有嬠
D┡=-Z┡。無底圓筒
C與它的上下邊界
W1與
W0按所標箭頭定向後有嬠
C=
W1-
W0(圖3)。在圖 4環面
T中,圓圈Z為曲面塊
A的邊緣,嬠
A=Z,這時稱閉曲線Z在環面
T上同調於零,記作Z~0。閉曲線
W在
T上不同調於零,但嬠
B=
W-
W1,這時稱閉曲線
W同調於
W1,記作
W~
W1。同調概念就是在這種定向圖形之間的邊緣關係上建立起來的。 在圖5的曲面
S上,
α、с、
d都不同調於零,
b)~0,
α不同調於с、
d中的任何一個,但с~
d。
 同調論
同調論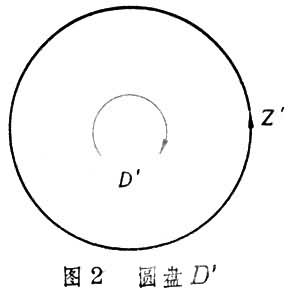 同調論
同調論 同調論
同調論將圖6中圓盤邊界上的每一對對徑點(諸如A與A┡,B與B┡)粘合,得到的曲面p叫做射影平面
在
p中為同一定向圓圈
z。可以看出,在
p中有
z+
z=2
z~0,但
z不同調於零。
 公式
公式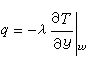 公式
公式H.龐加萊從1895年起,為了對同調概念做一般的討論,引進了可剖分為復形的空間,從此產生了組合拓撲學。
n維單形
0維單形是一個點,一維單形是一條線段,二維單形是一個三角形,三維單形是一個四面體,n維單形是一個具有n+1個頂點的廣義四面體。
定向單形
除0維單形不給定向外,其他維的單形可以有兩個定向。例如,一維單形的定向可以用從起點到終點的箭 頭給出,二維單形的定向可以用一個旋轉方向給出(圖7),等等。一般對於
n維單形有兩個定向,可以用頂點的順序來給出它的定向。彼此相差一個偶排列的兩個順序代表同一個定向。例如,線段
AB的一個定向可以用(
A,
B)表示,另一個定向則可用(
B,
A)表示;三角形
ABC的一個定向可用(
B,
A,
C)或(
C,
B,
A)或(
A,
C,
B)表示,另一個定向可用(
B,
C,
A,)或(
C,
A,
B)或(
A,
B,
C)表示。
 同調論
同調論單純復形
是由有限個單形很好地拼湊起來而組成的。例如,圖8之a這個單純復形是由4個0維單形
A,
B,
C,
D;4 個一維單形
AB,
BD,
CD,
BC和1個二維單形
BCD按照圖8之a中所畫的關係拼湊而組成的。圖8之b這個單純復形是由6個0維單形
A,
B,
C,
A┡,
B┡,
C┡,12個一維單形
AB,
BC,
CA,
A┡B┡,
B┡
C┡,
C┡
A┡,
B┡
C,
A┡
C,
A┡
B,
BB┡,
AA┡,
CC┡,6個二維單形
AA┡
B,
A┡
BB┡,
BB┡
C,
B┡
CC┡,
CC┡
A┡,
CA┡
A按照圖8之b中所畫的關係拼湊而組成的。
 同調論
同調論單純復形的
n維鏈 形 的線性組合叫一個
n維鏈,其中 }取遍單純復形
K的所有單形,且每個單形取好了定向(0維單形不取定向),αi為整數(即線性組合中的每一項是
K中的一個
n維定向單形,且附一個整係數)。兩個
n維鏈之和定義為一個
n維鏈,其每項的係數是兩個鏈的相應項的係數之和。容易驗證:
K的所有的
n維鏈組成一個交換群,這個交換群叫
K的
n維鏈群,記作
Cn(
K)。例如,圖8之a 中的單純復形,3(
A,
B)+2(
B,
C)-(
C,
D)-5(
B,
D)為一個一維鏈;圖8之b中的單純復形,4(
A,
A┡,
B)-2(
B,
B┡,
C)+(
C,
A,
A┡)為一個二維鏈。
 公式
公式 公式
公式邊緣運算元
規定0維單形的邊緣為零,一維定向單形(A,B)的邊緣為B-A,二維定向單形(A,B,C)的邊緣為(B,C)-(A,C)+(A,B),三維定向單形(A,B,C,D)的邊緣為(B,C,D)-(A,C,D)+(A,B,D)-(A,B,C),等等。可類似地定義n維定向單形的邊緣。以符號嬠寫在定向單形的前面表示它的邊緣。對於每一個n維
,規定它的邊 (即先取它的每一個定向單形的邊緣再乘上它的原來係數然後求和)。不難看出,一個
n維鏈的邊緣是一個
n-1維鏈。由此得到從
n維鏈群到
n-1維鏈群的同態,這個同態叫做(下)邊緣運算元,記作嬠:
Cn(
K)→
Cn-1(
K)。邊緣運算元具有嬠嬠=0的性質。
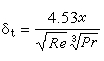 公式
公式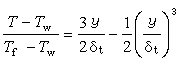 公式
公式n維閉鏈
滿足嬠x=0的n維鏈x叫n維閉鏈。例如,圖8a中的單純復形,一維鏈(C,D)-(B,D)+(B,C)就是一個一維閉鏈。單純復形K的所有n維閉鏈所組成的交換群叫K的n維閉鏈群,記作Zn(K)。
n維邊緣鏈
如果一個n維鏈是某一個 n+1維鏈的邊緣,則稱此鏈為n維邊緣鏈(即一個n維圖形是n+1維圖形的邊緣)。例如圖8a中的單純復形,一維鏈(C,D)-(B,D)+(B,C)=嬠(B,C,D)就是一個一維邊緣鏈。單純復形K的所有n維邊緣鏈所組成的交換群叫K的n維邊緣鏈群,記作Bn(K)。由於邊緣鏈一定是閉鏈,因而Bn(K)是Zn(K)的子群。
n維同調群
由於Bn(K)是 Zn(K)的子群,把商群Zn(K)/Bn(K)叫做單純復形K的n維(下)同調群,記作Hn(K)。Hn(K)中的每一個元素叫做一個n維同調類。如果兩個n維閉鏈zń,z怽的差為一個邊緣鏈時,就叫zń與z怽同調。如果zn是邊緣鏈,則稱zn同調於零。例如,圖8b中的單純復形,2個一維閉鏈(A,B)+(C,A)+(B,C),(A┡,B┡)+(C┡,A┡)+(B┡,C┡)有嬠((A,B,A┡)+(A┡,B,B┡)+(B,C,B┡)-(C,B┡,C┡)-(C,C┡,A┡)-(C,A┡,A))=((A,B)+(C,A)+(B,C))-((A┡,B┡)+(C┡,A┡)+(B┡,C┡))。因而這兩個閉鏈同調(而它們都不同調於零)。同調群 Hn(K)的秩叫做K的n維貝蒂數。如果在n維鏈群的定義中,用任意的一個交換群G中的元素代替整數,可以得到以G為係數的n維鏈群 Cn(K;G)。相似地有以G為係數的n維邊緣群Bn(K;G),n維閉鏈群Zn(K;G)。由此定義以G為係數的n維同調群Hn(K;G)。
多面體
單純復形 K的全體單形的並集叫做一個多面體,記作│K│。對於多面體的同調群Hn(|K|;G)可以用Hn(K;G)來定義,即令Hn(|K|;G)=Hn(K;G)。
單純映射 給定了兩個單純復形K,L,且指定了K的每一個頂點(0維單形)到L的某個頂點的一個對應,並把K中的屬於同一個單形的所有頂點對應到L的同在一個單形中的頂點,這個對應叫從K到L的單純映射。單純映射ƒ:K→L把 K中的每一個定向單形(頂點的一個順序)映射到L中的一個定向單形(得到對應頂點的一個順序,若有兩個頂點的像重合,則理解為對應到0),由此產生了一個從Cn(K;G)到 Cn(L;G)的同態,並且可以證明它把Zn(K;G)映射到Zn(L;G),Bn(K;G)映射到Bn(L;G)。從這個同態可以導出一個從Hn(K;G)到Hn(L;G)的同態。
同態
給了兩個多面體|K|、|L|之間的一個連續映射F:│K│→│L│,可以將K適當重分成另一復形K┡,並用一個單純映射去逼近F。利用這個單純映射導出的同調群之間的同態得到Hn(│K┡│;G)到Hn(│L│;G)的同態,並且可以證明,Hn(│K┡│;G)與Hn(|K|;G)自然地同構。 於是記此同態為Fn:Hn(|K|;G)→Hn(│L│;G)。
上同調群
G為任一交換群,Hom(Cn(K),G)為所有從Cn(K)到G的群同態所組成的群,這個群叫做K的以G為係數的 n維上鏈群,記作Cn(K;G)。利用K 的邊緣運算元嬠:Cn(K)→Cn-1(K)可得對偶同態δ:Cn-1(K;G)→Cn(K;G)。定義如下:設ƒ∈Cn-1(K;G),規定δƒ=ƒ嬠:Cn(K)→G。這個δ叫上邊緣運算元,具有δδ=0的性質。與同調群的定義相似,可以定義以G為係數的上閉鏈群Zn(K;G),上邊緣鏈群Bn(K;G),上同調群Hn(K;G)。當G為整數加群Z時,省去符號Z,簡單記為 Cn(K),Zn(K),Bn(K),Hn(K),等等。對於連續映射F:│K│→│L│,利用單純映射去逼近,可得到同態。上同調群的構造可以由同調群完全確定。當多面體│K│為定向流形時,同調群和上同調群之間還有對偶關係(流形的龐加萊對偶定理),即Hn(|K|;G)同構於Hq-n(│K│;G),其中q為流形│K│的維數。
J.W.亞歷山大在1915年證明了多面體的同調群的拓撲不變性,即如果兩個多面體│K│,│L│同胚,那么這個同胚誘導它們的上同調群、同調群的同構。實際上,如果│K│,│L│倫型相同,其同倫等價也誘導它們的上同調群、同調群的同構。
利用同調群可以解決不少幾何問題。例如,布勞威爾不動點定理(見
不動點理論),可以找到歐拉示性數與貝蒂數之間的關係式:
其中αi為復形
K的
i維單形個數,
b)i為多面體│
K│的
i維貝蒂x(
K)即
K的歐拉示性數。從而證明了歐拉示性數是│
K│的拓撲不變數。
 公式
公式單純復形的整係數同調群是個有限生成的交換群。因此,它同構
,其中Z代表整數加群,
θ(1,
n),…,
θ(τn,
n)為一串自然數,每個可整除後一個,嘰表示直和。前面Z的個數即為
n維貝蒂數;後面這串有限群的階數
θ(1,
n),…,
θ(τn,
n)稱為
n維撓係數。確定一個單純復形(及其多面體)的各維貝蒂數與撓係數,也就算出了同調群。
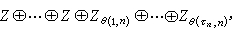 公式
公式簡單的單純復形的同調群的計算,可以通過叫做"擠到邊上去"的方法直觀地解決。一般單純復形同調群的計算,可以用矩陣變換的方法經有限多次的算術運算解決,不過具體實現這種計算是非常困難的。
帶係數群G的同調群的構造,可由整係數同調群與G按照“泛係數”公式來求。上同調群的計算也有其相應的公式。
同調論的公理
S.艾倫伯格和N.E.斯廷羅德提出了同調群、上同調群滿足的公理,並證明了在多面體的情形下滿足公理的同調群、上同調群是惟一的。
在一般的拓撲空間上引進同調群主要有兩種方式。利用有序單形映射到拓撲空間,來定義這個拓撲空間的同調群,稱為這個拓撲空間的奇異同調群;利用單純復形來逼近一個拓撲空間,用極限來定義這個拓撲空間的同調群,稱為這個拓撲空間的切赫同調群。在緊多面體的情況,這兩種同調群都同構於按單純剖分得到的同調群。
在以某種環為係數的上同調群中可以引入乘法使之成為上同調環。為了更好地利用上同調群,在其上引入了所謂上同調運算的額外結構,例如斯廷羅德冪,龐特里亞金冪等等。由斯廷羅德冪發展成為斯廷羅德代數的研究,大大豐富了同調論的內容。
 同調論
同調論 同調論
同調論 同調論
同調論 同調論
同調論 同調論
同調論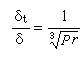 公式
公式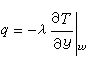 公式
公式 同調論
同調論 同調論
同調論 公式
公式 公式
公式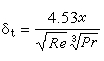 公式
公式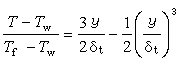 公式
公式 公式
公式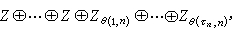 公式
公式