幾乎處處收斂是處處收斂概念的推廣。設 X 是隨機變數,{Xn}是隨機變數序列,如果P(Xn→X)=1(n→∞),則稱Xn幾乎處處收斂於X。
基本介紹
- 中文名:幾乎處處收斂
- 外文名:convergence almost everywhere
- 適用範圍:數理科學
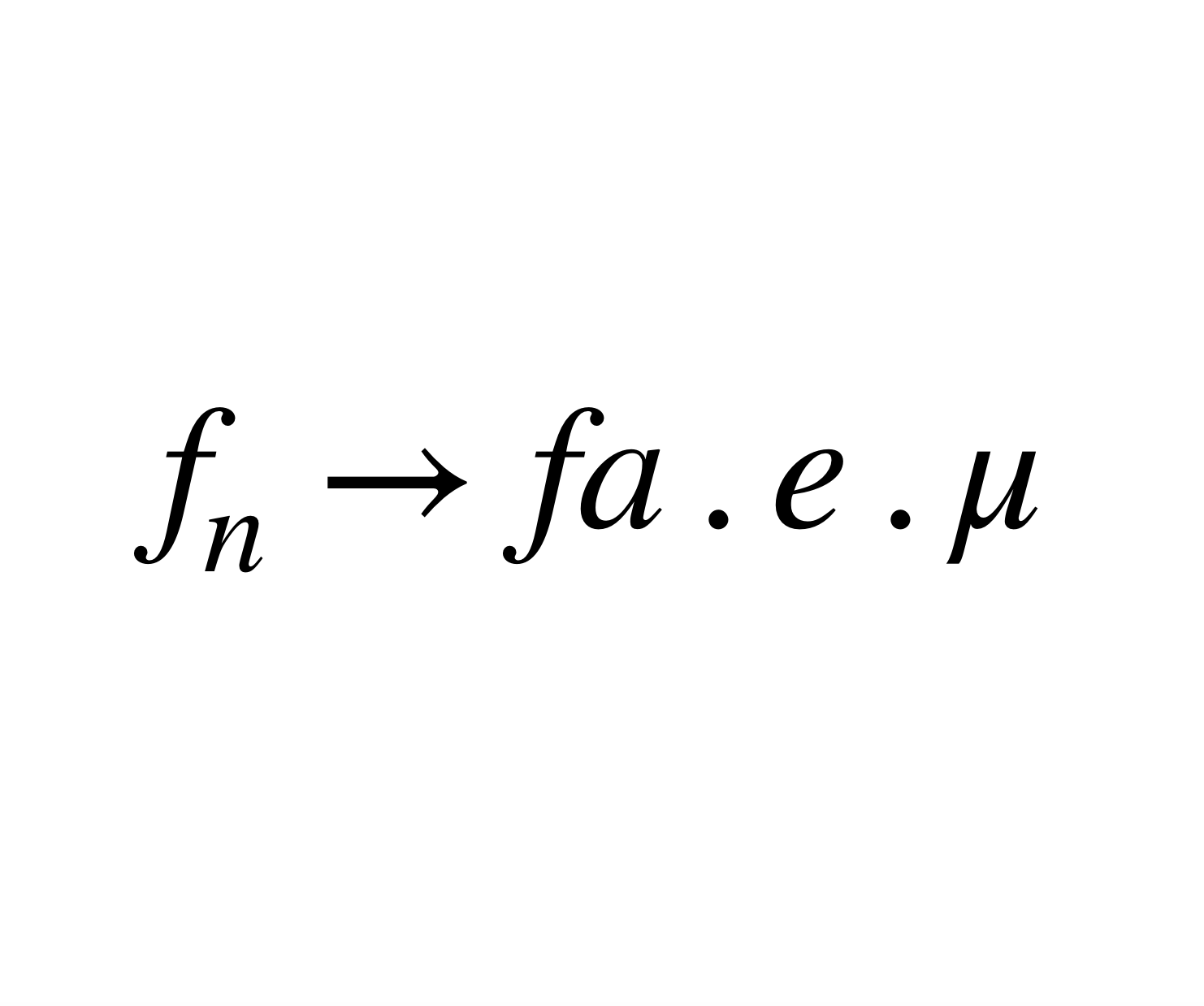
幾乎處處收斂是處處收斂概念的推廣。設 X 是隨機變數,{Xn}是隨機變數序列,如果P(Xn→X)=1(n→∞),則稱Xn幾乎處處收斂於X。
幾乎處處收斂是處處收斂概念的推廣。設 X 是隨機變數,{Xn}是隨機變數序列,如果P(Xn→X)=1(n→∞),則稱Xn幾乎處處收斂於X。...
亦稱幾乎處處收斂、殆必收斂。 ...... 亦稱幾乎處處收斂、殆必收斂。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第75頁 V百科往...
則稱 依測度 μ 收斂(convergence in measure μ)於f,記為 。若在X的一個 測度為0的子集外,對 ,均有則稱 則稱關於測度μ幾乎處處收斂(convergence almost ...
以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然...
三級數定理是機率論中判定隨機變數和的序列幾乎處處收斂的重要定理。三級數定理給出了隨機變數和序列幾乎處處收斂的必要條件和充分條件。...
大數律,即大數定律,是機率論中討論隨機變數序列的算術平均值向常數收斂的定律,...幾乎處處收斂與依機率收斂不同。生活例子:開始上課了,慢慢地大家都安靜下來,這...
幾乎處處收斂至f。從葉戈羅夫定理可知,除了一個測度任意小的開集外, 一致收斂至f。因為連續函式的一致收斂極限仍是連續的,故此f在此開集外連續。取E為以上兩個開...
②是否所有連續函式的傅立葉級數都幾乎處處收斂?把問題集中到連續函式,這就反映了一定程度的傾向性,即認為原來的盧津猜想未必成立。可是改變後的盧津問題的證明仍...
該定理說明,在A上幾乎處處逐點收斂,意味著除了在任意小測度的某個子集B上外一致收斂。這種收斂又稱為幾乎一致收斂。葉戈羅夫定理假設的討論 編輯 ...
平均遍歷定理斷定:對於平方可積的函式ƒ,時間平均的極限在平均收斂的意義下存在,滿足f(φ(x))=f(x)(幾乎處處成立)和。個體遍歷定理斷定:對於可積函式ƒ,...
1913年俄國數學家Η.Η.盧津在他發表的一篇論文中,提出了如下的猜想:區間【0,2π】上平方可積函式的傅立葉級數,在【0,2π】上幾乎處處收斂。這個猜想經過半...
幾乎處處收斂於E,則列維定理可測函式 編輯 設f是定義在可測集E上的實函式。如果對每一個實數,集E[f>a]恆可測(勒貝格可測),則稱f是定義在 E上的(勒貝格...
測度論收斂 編輯 同L測度一樣,在測度空間(Χ,φ,μ)中也有命題P在E上“幾乎處處”成立的概念,它是指E中使命題P不成立的點的全體(它可能不是可測集)包含在...
第一條強大數定律(strong law of large numbers)是由波萊爾在1909年對伯努利試驗場合驗證的,給出了幾乎處處收斂的隨機變數列的性質。強大數定律主要包括波萊爾強大數...
幾乎處處收斂與依機率收斂不同。生活例子:開始上課了,慢慢地大家都安靜下來,這是幾乎處處收斂。絕大多數同學都安靜下來,但每一個人都在不同的時間不安靜,這是依...
2.當t是x(t)的間斷點時,級數收斂於 。1966年,里納特·卡爾松證明了勒貝格二次可積函式的傅立葉級數一定是幾乎處處收斂的,即級數在除了一個勒貝格零測集外均...
6.1 級數收斂定理6.2 大數定律6.3 kolmogorov重對數律習題6第7章 離散鞅論7.1 鞅的基本概念7.2 鞅不等式和鞅的幾乎處處收斂性...
