盧津問題,數學研究術語,又稱盧津猜想,是傅立葉級數理論中的一個著名問題。
基本介紹
- 中文名:盧津問題
- 類型:數學研究術語
- 又稱:盧津猜想
- 簡介:傅立葉級數理論中的一個著名問題
正文,
正文
又稱盧津猜想,傅立葉級數理論中的一個著名問題。1913年俄國數學家Η.Η.盧津在他發表的一篇論文中,提出了如下的猜想:區間【0,2π】上平方可積函式的傅立葉級數,在【0,2π】上幾乎處處收斂。這個猜想經過半個多世紀許多數學家的努力,終於被瑞典數學家L.卡爾森於用非常深刻的數學方法所證實。
傅立葉級數理論是19世紀初,從關於熱傳導的研究中產生的。中心問題是:怎樣的函式可以用它的傅立葉級數來表示?隨著勒貝格測度、勒貝格積分理論的創立,傅立葉級數的幾乎處處收斂問題逐漸為人們所重視。1906年,P.J.L.法圖首先證明,假如 W(n)=n,
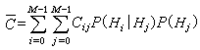
C是絕對常數。最後,於1966年,卡爾森利用哈代-李特爾伍德極大函式和考爾德倫的上述原理,以十分精巧的數學論證,證實了盧津猜想。
