平行平面定理(theorem of parallel planes)是立體幾何的重要定理之一。如果一個平面與兩個平行平面同時相交,則在形成的三面八角幾何圖形中:1.同位二面角相等;2.內錯二面角相等;3.外錯二面角相等;4.同旁內二面角互補;5.同旁外二面角互補。
基本介紹
- 中文名:平行平面定理
- 外文名:theorem of parallel planes
- 所屬學科:數學(空間幾何)
- 相關概念:平行平面,二面角等
基本介紹
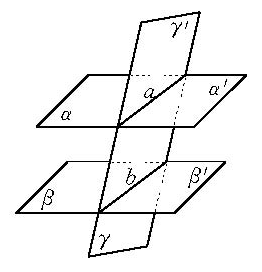 圖1
圖1

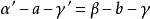
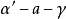

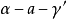

定理的證明
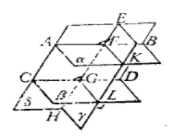 圖2
圖2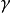
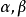
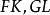
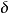
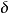

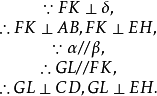
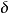
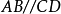

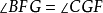
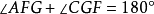







平行平面定理(theorem of parallel planes)是立體幾何的重要定理之一。如果一個平面與兩個平行平面同時相交,則在形成的三面八角幾何圖形中:1.同位二面角相等;2.內錯二面角相等;3.外錯二面角相等;4.同旁內二面角互補;5.同旁外二面角互補。
 圖1
圖1

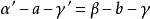
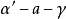

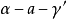

 圖2
圖2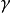
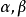
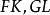
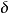
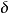

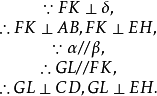
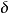
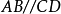

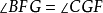
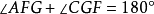






平行平面定理(theorem of parallel planes)是立體幾何的重要定理之一。如果一個平面與兩個平行平面同時相交,則在形成的三面八角幾何圖形中:1.同位二面角相等;2.內...
平行平面截直線定理,是指兩條直線穿過一組平行平面,則其各平面的交點所組成的線段成比例的一個立體幾何定理。...
空間三線平行定理(theorem of three parallel lines in space)是立體幾何的基本定理之一。如果兩條直線分別與第三條直線平行,則這兩條直線也互相平行,這一定理反映...
平行軸定理(parallel axis theorem)能夠很簡易地,從剛體對於一支通過質心的直軸(質心軸)的轉動慣量,計算出剛體對平行於質心軸的另外一支直軸的轉動慣量。...
面面平行,指的是兩個平面平行。如果兩個平面沒有公共點,則稱這兩個平面平行。如果兩個平面的垂線平行,那么這兩個平面平行。如果一個平面內有兩條相交直線與另...
兩平面平行(parallelism between two planes)是兩平面間的一種位置關係,如果兩個平面沒有公共點,則稱這兩個平面有平行位置關係,簡稱兩平面相互平行,一個平面稱為...
線面平行,幾何術語。定義為一條直線與一個平面無公共點(不相交),稱為直線與平面平行。...
平面上兩條直線、空間的兩個平面或空間的一條直線與一平面之間不相交時的關係。平行線永不相交。...
空間平行角定理(theorem of parallel angles inspace)是立體幾何的基本定理之一。對於空間兩個不相同的角,如果它們的兩組對應邊分別平行,則這兩個角相等或互補。....
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。...
平行線分線段成比例定理指的是兩條直線被一組平行線(不少於3條)所截,截得的對應線段的長度成比例。推論:平行於三角形一邊的直線,截其他兩邊(或兩邊延長線)所...
在同一個二維平面內,由兩組平行線段組成的閉合圖形,稱為平行四邊形,其邊與邊、角與角、對角線之間存在著各種各樣的關係,即是平行四邊形性質定理。...
平面幾何公理描述 編輯 《幾何原本》開篇的第一個定理 歐幾里得幾何的傳統描述是...19世紀,通過構造非歐幾里得幾何,說明平行公理是不能被證明的(若從上述公理體系中...
直角射影定理(projection theorem of a rightangle to a plane)是立體幾何的重要定理之一,一直角在平面上的(正)射影為直角的充分必要條件是:原直角至少有一邊...
達朗貝爾定理是關於變換的著名定理。該定理斷言:每個...在n維歐氏空間(包括普通平面和空間)中,也把保持兩點...是一個旋轉與一個平移之積,且旋轉軸平行於這平移...
凸集分離定理是凸集理論的最基本的定理,它是指在很弱的條件下,兩個不相交的凸集總可用超平面分離。...
1、通過真命題(公理或其他已被證明的定理)出發,經過受邏輯限制的演繹推導,證明為正確的結論的命題或公式,例如“平行四邊形的對邊相等”就是平面幾何中的一個定理...
平面把(bundle of planes)亦稱平面叢,是一種空間圖形,空間一定點的所有平面組成的集合稱為平面把。這個定點稱為平面把的中心,另一種平面把是平行於同一條直線(...
沙勒定理(Chasles theorem)關於變換的著名定理,該定理斷言:既非旋轉也非平移的空間第一種契約變換是一個旋轉與一個平移之積,且旋轉軸平行於這平移的方向。簡言之,...
門納勞斯定理(Menelaus theorem)是關於共線點的一個重要定理,設X,Y,Z分別是△...卷Ⅰ的主要內容是比較球面與平面這兩種三角形的異同,力圖平行於歐幾里得《幾何...
(2)一條直線垂直於平面,定義這直線與平面所成的角是直角(3)一條直線和平面平行,或在平面內,定義它和平面所成的角是00的角三垂線定理 在平面內的一條直線,...
