空間三線平行定理(theorem of three parallel lines in space)是立體幾何的基本定理之一。如果兩條直線分別與第三條直線平行,則這兩條直線也互相平行,這一定理反映空間中彼此不同的直線平行關係的傳遞性。
基本介紹
- 中文名:空間三線平行定理
- 外文名:theorem of three parallel lines in space
- 所屬學科:數學
- 所屬問題:空間幾何
- 簡介:平行於同一條直線的兩條直線平行
基本介紹,空間三線平行定理的證明,例題解析,
基本介紹
空間三線平行定理 平行於同一條直線的兩條直線互相平行。
如圖1,若a、b、c是不在同一個平面內的三條直線,a//b,a//c,則b//c。
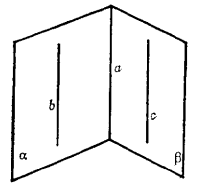 圖1
圖1空間三線平行定理的證明
已知直線a//b,c//b。
求證 a//c。
證明 ①當三直線a,b,c共面時,這定理是平面幾何中的定理,用反證法證明,圖2。
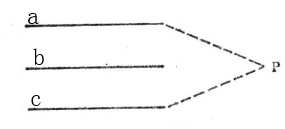 圖2
圖2∵在同一平面內的兩條不相重合的直線,它們的相互位置關係只可能有兩種:平行或相交,假定a不平行於c,那么a和c必相交於一點P。
又∵ 已知a//b,c//b,即經過P點有兩條直線都和EF平行。這和平行公理相矛盾。
所以a和c相交的假定是錯的。那么只有a//c成立。
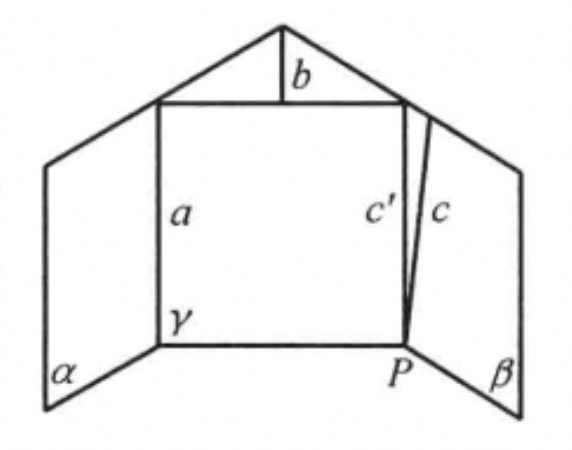
②當a,b,c不共面時,過a,b所確定的平面α與過直線b,c所確定的平面β相交於b,在c上任取一點P(如圖3),設a,P所確定的平面γ與β相交於c',則c'與a可能相交或平行。
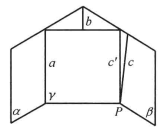 圖3
圖3若c'與a相交於點M,則點M在α,β內,必在b上,與a//b矛盾。
若c'與a平行,且c'與b不平行,可設c與b相交於點Q,則點Q在γ,α內,必在α上,這與c'//a矛盾,所以c'//b。
因為c'∩c=P,c'//b,c//b,所以c'與c重合(平行公理),故c與a平行。
例題解析
【例1】空間的兩個角,如果對應邊同向平行,則這兩個角相等。
已知:∠BAC和∠B'A'C'為空間兩個角,AB//A'B',AC//A'C',且方向相同。
求證:∠BAC=∠B'A'C'。
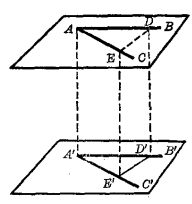 圖4
圖4證明:分別在∠BAC與∠B'A'C'的兩邊截取AD= A'D',AE= A'E',
∵AD平行且等於A'D',
∴AA'D'D是平行四邊形,
∴AA'平行且等於DD',
又∵AE平行且等於A'E',
∴AA'E'E是平行四邊形,
∴AA'平行且等於EE',
於是DD'平行且等於EE'(三線平行定理),從而ED= E'D',
∴△ADE≌△A'D'E',
∴∠BAC= ∠B'AC'.