兩平面平行(parallelism between two planes)是兩平面間的一種位置關係,如果兩個平面沒有公共點,則稱這兩個平面有平行位置關係,簡稱兩平面相互平行,一個平面稱為另一個平面的平行平面。
基本介紹
- 中文名:兩平面平行
- 外文名:parallelism between two planes
- 所屬學科:數學
- 所屬問題:立體幾何
- 特點:兩個平面沒有公共點
兩平面平行的定義
兩平面平行的性質定理
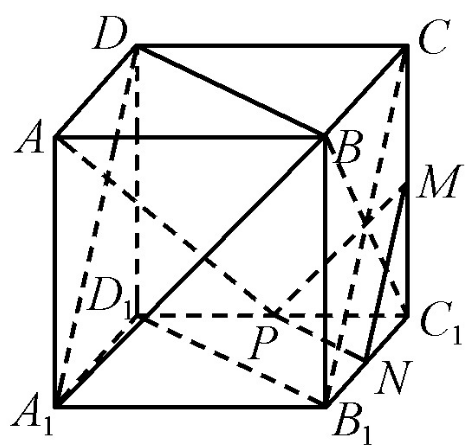 圖1
圖1兩平面平行的判定





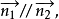
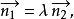



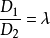











 圖2
圖2




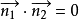

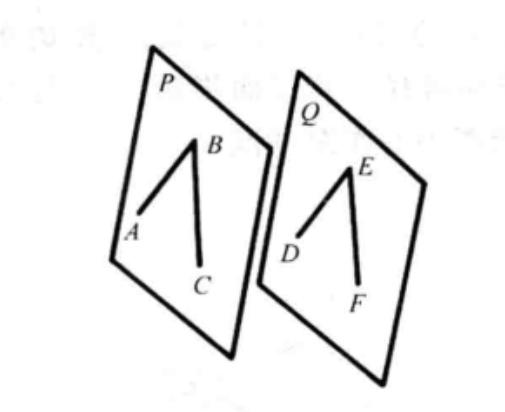
兩平面平行(parallelism between two planes)是兩平面間的一種位置關係,如果兩個平面沒有公共點,則稱這兩個平面有平行位置關係,簡稱兩平面相互平行,一個平面稱為另一個平面的平行平面。
 圖1
圖1




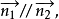
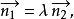



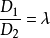











 圖2
圖2




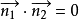

兩平面平行(parallelism between two planes)是兩平面間的一種位置關係,如果兩個平面沒有公共點,則稱這兩個平面有平行位置關係,簡稱兩平面相互平行,一個平面稱為...
平行平面定理(theorem of parallel planes)是立體幾何的重要定理之一。如果一個平面與兩個平行平面同時相交,則在形成的三面八角幾何圖形中:1.同位二面角相等;2.內...
在平面上兩條直線、空間的兩個平面以及空間的一條直線與一平面之間沒有任何公共點時,稱它們平行。如圖直線AB平行於直線CD,記作AB∥CD。平行線在無論多遠都不...
兩平面相交(intersection between two planes)是兩平面間的一種位置關係,如果兩個平面只有一條公共直線,就說這兩個平面有相交位置關係,簡稱兩平面相交。這兩個平面...
平行度指兩平面或者兩直線平行的程度,指一平面(邊)相對於另一平面(邊)平行的誤差最大允許值。平行度評價直線之間、平面之間或直線與平面之間的平行狀態。其中一個...
平面外的一條直線與此平面內的一條直線平行,則該直線與此平面平行。平面平面平行的判定 一 如果一個平面內有兩條相交直線都平行於另一個平面,那么這兩個平面...
平行平面截直線定理,是指兩條直線穿過一組平行平面,則其各平面的交點所組成的線段成比例的一個立體幾何定理。...
平面上兩條直線、空間的兩個平面或空間的一條直線與一平面之間不相交時的關係。平行線永不相交。...
超平行平面亦稱羅氏空間的離散平面,是羅氏空間中兩平面的一種位置關係。若兩個平面,其中沒有一個包含著平行於另一個平面的直線,則這兩個平面稱為離散的。兩個...
投影面平行面是一類具有特殊位置的平面。指平行某一投影面,而與另外兩個投影面垂直的平面。...
幾何中,在同一平面內,永不相交(也永不重合)的兩條直線(line)叫做平行線(parallel lines)。平行線公理是幾何中的重要概念。歐氏幾何的平行公理,可以等價的陳述為...
平行線是指在同一平面內永不相交的兩條直線,判定平行線的方法包括1.同位角相等,兩直線平行2.內錯角相等,兩直線平行3.同旁內角互補,兩直線平行。...
平行平面法(parallel plane method)一種優選方法.首先任取一個因素,在兩個平行平面上用雙因素優選法找出最好的點,切掉其餘部分,留下好點所在的那個部分,然後繼續...
側平面(profile plane)是一種投影面平行面,平行於側投影面(W面)的平面稱為側平面。平行於正投影面(V面)的投影面叫正平面,平行於水平面(H面)的平面叫水平面...
在平面上兩條直線、空間的兩個平面以及空間的一條直線與一平面之間沒有任何公共點時,稱它們平行。如圖直線AB平行於直線CD,記作AB∥CD。平行線在無論多遠都不...
互相平行,數學名詞,指的是平面內,兩條直線永不相交。...... 互相平行,數學名詞,指的是平面內,兩條直線永不相交。中文名 互相平行 所屬學科 高等數學 原理 ...
推論一:經過一條直線和直線外的一點,有且只有一個平面。推論二:經過兩條相交直線,有且只有一個平面。推論三:經過兩條平行直線,有且只有一個平面。...
定義:若兩個平面的二面角為直二面角(平面角是直角的二面角),則這兩個平面互相垂直。...
