平行四邊形四邊對角線平方和定理,平行四邊形的四條邊的邊長的平方和等於對角線長的平方和。
基本介紹
- 中文名:平行四邊形四邊對角線平方和定理
- 表達式:AC + BD = 2AB + 2BC
- 適用領域:幾何
- 套用學科:數學

平行四邊形四邊對角線平方和定理,平行四邊形的四條邊的邊長的平方和等於對角線長的平方和。

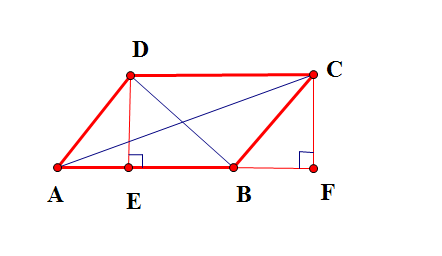
平行四邊形四邊對角線平方和定理,平行四邊形的四條邊的邊長的平方和等於對角線長的平方和。引證解釋方法一:設平行四邊形ABCD,作DE⊥AB於E,CF⊥AB,交AB延長線於F∵ 四邊形 ABCD 是平行四邊形∴ AB//DC...
四邊邊長的平方和等於兩條對角線的平方和。分類 矩形、菱形、正方形是特殊的平行四邊形。判定定理 (1)定義法:兩組對邊分別平行的四邊形是平行四邊形;(2)兩組對邊分別相等的四邊形是平行四邊形;(3)兩組對角分別相等的四邊形是平行四邊形;(4)對角線互相平分的四邊形是平行四邊形;(5)一組對邊平行且...
邊的長度的平方一樣,都是:邊和 邊的長度的平方一樣。根據勾股定理,可以算出:同樣的,根據勾股定理,也可以算出對角線{\displaystyle AC}的長度的平方為:而對角線 的長度的平方則是:於是平行四邊形四邊長度的平方和等於:而平行四邊形的兩條對角線長度的平方和則等於:可以看到,兩者是一樣的。賦范內積空間...
(12)平行四邊形ABCD中,AC、BD是平行四邊形ABCD的對角線,則各四邊的平方和等於對角線的平方和。(13)平行四邊形對角線把平行四邊形面積分成四等份。(14)平行四邊形中,兩條在不同對邊上的高所組成的夾角,較小的角等於平行四邊形中較小的角,較大的角等於平行四邊形中較大的角。(15)平行四邊形的面積...
長×長+寬×寬=對角線×對角線(其實就是勾股定理)即兩個直角邊的平方和等於斜邊的平方。狹義的對角線,是在多邊形中任意兩個非鄰接的頂點的連線(線段).廣義的對角線,是在多維度體中任意兩個非鄰接的頂點的連線(線段).代數 行列式 在n階行列式中,從左上至右下的數歸為主對角線,從左下至右上的數歸...
廣義勾股定理 廣義勾股定理(Generalized Pythagorean theorem)指勾股定理的推廣。套用 這是普通勾股定理即2維歐幾里得空間且向量a的範數定義為 ||a||=(x2+y2)1/2(或者||a||=ata)1/2(列向量a的轉置與a的矩陣乘積的1/2次方)的推廣。
平行四邊形定則是數學科的一個定律。兩個向量合成時,以表示這兩個向量的線段為鄰邊作平行四邊形,這個平行四邊形的對角線就表示合向量的大小和方向,這就叫做平行四邊形定則(Parallelogram law)。發展簡史 1586年,荷蘭的斯蒂文在《靜力學基礎》一書中最早提出力的分解與合成原理,並把這一原理(沒有明確表達出...
(簡述為“平行四邊形的鄰角互補”)(4)夾在兩條平行線間的平行線段相等。(5)如果一個四邊形是平行四邊形,那么這個四邊形的兩條對角線互相平分。(簡述為“平行四邊形的對角線互相平分”)判定 (1)如果一個四邊形的兩組對邊分別相等,那么這個四邊形是平行四邊形。(簡述為“兩組對邊分別相等的四邊形是...
學習平行四邊形對角線特徵及運用,解決老人分平行四邊形土地給四個孩子問題。設計思路 1、複習已學平行四邊形的性質;2、由“老人分平行四邊形土地給四個孩子”問題引入;3、學習平行四邊形對角線特徵——平行四邊形對角線互相平分;4、平行四邊形的對角線特徵的運用,解決老人分平行四邊形土地給四個孩子是否合理的...
在幾何形狀中,阿波羅尼奧斯定理表示三角形兩邊平方的和,等於所夾中線及第三邊之半的平方和的兩倍。具體來說,在任何三角形 中,如果 是中線,那么 這是一個特殊情況的斯圖爾特定理。對於 的等腰三角形,的中線垂直於 ,定理簡化為三角形ADB(或三角形ADC)的畢達哥拉斯定理。從平行四邊形的對角線相互平分的事實...
7.平行六面體的每一對角線長的平方等於共一端點的三條棱長的平方和減去這二條棱中每兩條棱長及其所夾角餘弦之積的兩倍。8.平行六面體的每一對角線通過與該對角線共端點的三條棱的另一端點構成的三角形截面的重心,且被這三角形截面分成三等分。9.平行六面體的每個由三條側面對角線構成的三角形截面面積平方的4...
互逆定理典例 1、直角三角形中,兩直角邊的平方和等於斜邊的平方。(勾股定理)其逆定理:如果三角形的三邊長a,b,c滿足a²+b²=c²,那么這個三角形是直角三角形。2、平行四邊形的對角線互相平分。其逆定理:如果一個四邊形對角線互相平分,那么這個四邊形是平行四邊形。3、角平分線上的點到角的兩邊的...
很多與平行公設等價的命題,似乎與平行線無關。有些性質更看似很明顯,因而被一些聲稱證明了平行公設的人不經意用到了。這裡是一些命題:三角形內角和為兩直角。所有三角形的內角和都相等。存在一對相似但不全等的三角形。所有三角形都有外接圓。.若四邊形三個內角是直角,那么第四個內角也是直角。存在一對等距的...
根據平行四邊形定律(兩對角線的平方和等於一組臨邊平方和的兩倍),有:把(1)和(2)代入,有 故有 ,唯一性得證。在此基礎上,可以給出凸集分離定理的證明。定理證明 因為 為非空集合,是 外的一點,故由引理知,存在一點 ,使得 設 ,那么因 為凸集,故有 ,使 因此,上式兩邊的 可消去,得 在上...
互逆定理典例 1、直角三角形中,兩直角邊的平方和等於斜邊的平方。(勾股定理)其逆定理:如果一個三角形兩邊的平方和等於第三邊的平方,那么這個三角形是直角三角形。最長邊所對的角為直角。2、平行四邊形的對角線互相平分。其逆定理:如果一個四邊形對角線互相平分,那么這個四邊形是平行四邊形。3、角平分線上...
∴a²+b²-c²=2ab*cosC(正弦定理)∴c²=a²+b²-2ab*cosC 平面向量證法 ∵如圖6,有a+b=c(平行四邊形定則:兩個鄰邊之間的對角線代表兩個鄰邊大小)∴c·c=(a+b)·(a+b)∴c²=a·a+2a·b+b·b∴c²=a²+b²+2|a||b|cos(π-θ)(以上粗體字元表示向量)又...
53、平行四邊形性質定理2 :平行四邊形的對邊相等 54、推論 :夾在兩條平行線間的平行線段相等 55、平行四邊形性質定理3 :平行四邊形的對角線互相平分 56、平行四邊形判定定理1 :兩組對角分別相等的四邊形是平行四邊形 57、平行四邊形判定定理2 :兩組對邊分別相等的四邊形是平行四邊形 58、平行四邊形判定定理...
53平行四邊形性質定理2 平行四邊形的對邊相等 54推論 夾在兩條平行線間的平行線段相等 55平行四邊形性質定理3 平行四邊形的對角線互相平分 56平行四邊形判定定理1 兩組對角分別相等的四邊形是平行四邊形 57平行四邊形判定定理2 兩組對邊分別相等的四邊形是平行四邊形 58平行四邊形判定定理3 對角線互相平分的四邊形...
53平行四邊形性質定理2 平行四邊形的對邊相等 54推論 夾在兩條平行線間的平行線段相等 55平行四邊形性質定理3 平行四邊形的對角線互相平分 56平行四邊形判定定理1 兩組對角分別相等的四邊形是平行四邊形 57平行四邊形判定定理2 兩組對邊分別相等的四邊形是平行四邊形 58平行四邊形判定定理3 對角線互相平分的四邊形...
①合力和力的合成:一個力產生的效果如果能跟原來幾個力共同作用產生的效果相同,這個力就叫那幾個力的合力,求幾個力的合力叫力的合成. 2.力的平行四邊形定則:求兩個互成角度的共點力的合力,可以用表示這兩個力的線段為鄰邊作平行四邊形,合力的大小和方向就可以用這個平行四邊形的對角線表示出來。 ②共點的...
直角三角形:(1)直角三角形的兩個銳角互余。(2)直角三角形兩直角邊的平方和等於斜邊的平方,表達式為a²+b²=c²。(勾股定理)四邊形 不同四邊形的定義 基本定義:由不在同一直線上的四條線段依次首尾相接圍成的封閉的平面圖形或立體圖形叫四邊形。平行四邊形:兩組對邊分別平行的四邊形是平行四邊形。矩...
正方形,是特殊的平行四邊形之一。即有一組鄰邊相等,並且有一個角是直角的平行四邊形稱為正方形,又稱正四邊形。正方形,具有矩形和菱形的全部特性。定義 有一個角是直角且有一組鄰邊相等的平行四邊形是正方形。性質 判定定理 1:對角線相等的菱形是正方形。2:有一個角為直角的菱形是正方形。3:對角線互相...
分析:首先根據△AOB是等邊三角形及平行四邊形對角線互相平分的性質判定出ABCD是矩形,再利用勾股定理計算邊長,從而得到面積。例2:已知:如圖2,在ABCD中,M為BC中點,∠MAD=∠MDA.求證:四邊形ABCD是矩形。分析:根據定義去證明一個角是直角,由△ABM≌DCM(SSS)即可實現。證明:因為平行四邊形ABCD 故:AB=CD,...
53平行四邊形性質定理2 平行四邊形的對邊相等 54推論 夾在兩條平行線間的平行線段相等 55平行四邊形性質定理3 平行四邊形的對角線互相平分 56平行四邊形判定定理1 兩組對角分別相等的四邊形是平行四邊形 57平行四邊形判定定理2 兩組對邊分別相等的四邊形是平行四邊形 58平行四邊形判定定理3 對角線互相平分的四邊形...
把兩個矢量首尾相接從而求出和矢量的方法,叫做三角形定則。力是矢量,求兩個力的合力時,不能簡單把兩個力相加,而按三角形定則來確定力的大小和方向。平行四邊形 兩個力合成時,以表示這兩個力的線段為鄰邊作平行四邊形,這兩個鄰邊之間的對角線就代表合力的大小和方向,這就叫做平行四邊形定則(parallelogram ...
