平行四邊形恆等式

在數學中，平行四邊形恆等式是描述平行四邊形的幾何特性的一個恆等式。它等價於三角形的中線定理。在一般的賦范內積空間（也就是定義了長度和角度的空間）中，也有類似的結果。這個等式的最簡單的情形是在普通的平面上：一個平行四邊形的兩條對角線長度的平方和，等於它四邊長度的平方和。

基本介紹

• 中文名：平行四邊形恆等式
• 外文名：Parallelogram law
• 分類：數理科學

簡介

假設這個平行四邊形是寫作 的話，那么平行四邊形恆等式就可以寫成：

當平行四邊形是矩形的時候，由矩形的幾何特性可以知，這時兩條對角線是一樣長的。所以平行四邊形恆等式變為：

也就是直角三角形的勾股定理：

也就是說，平面上的平行四邊形恆等式可以看成是勾股定理的一種推廣。

一般四邊形的情況

對於一般的四邊形，平行四邊形恆等式不再成立，但可以得到的是一個相似的不等式：

用一般的語言來說，就是一般四邊形的四條邊長度的平方和總是大於或者等於兩條對角線長度的平方和。一個更加精確的結果是：

其中的{\displaystyle x}是兩條對角線的中點連成的線段的長度。

複平面情形

在複平面上，可以將平行四邊形恆等式寫為複數的形式。

使用勾股定理的證明

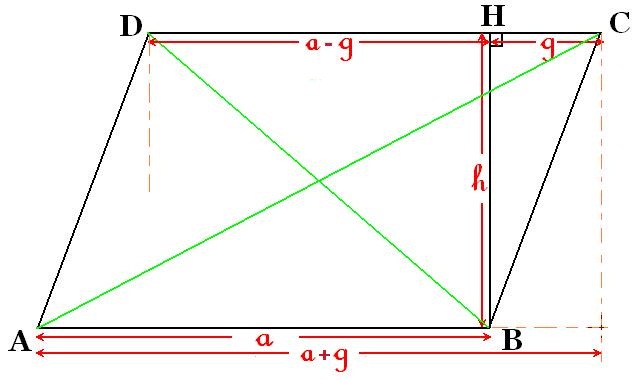
圖1 平行四邊形

如圖1，在平行四邊形 中，設邊 的長度為 ，過點 作垂直於 的直線交線段 於 ，設線段 的長度（即 對應的高）為 ，線段 的長度為 。那么

邊和邊的長度的平方一樣，都是：

邊和邊的長度的平方一樣。根據勾股定理，可以算出：

同樣的，根據勾股定理，也可以算出對角線{\displaystyle AC}的長度的平方為：

而對角線的長度的平方則是：

於是平行四邊形四邊長度的平方和等於：

而平行四邊形的兩條對角線長度的平方和則等於：

可以看到，兩者是一樣的。

賦范內積空間上的推廣

更一般的，在高維的歐幾里得空間中（比如在三維空間中），可以想像平行四邊形恆等式仍然是成立的，因為總可以找到平行四邊形所在的平面，然後用平面上的方法證明。而在更廣泛的定義了內積（初等幾何中“角度”概念的推廣，記作）和相應的範數（初等幾何中“長度”概念的推廣，記作）的線性空間中，儘管已經沒有直觀幾何意義上的平行四邊形的概念，但仍然會有類似的恆等式：

也就是說，兩個向量的和與差的“長度”（範數）的平方和等於它們自己的“長度”的平方和的兩倍。

如果是沒有定義內積，僅僅有範數的線性空間，則不一定有這樣的結果。如果線性空間上定義的範數不是與某個內積相聯繫（）的話，那么上面的等式將不再成立。

使用內積和範數的證明