常微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。
基本介紹
- 中文名:常微分運算元
- 外文名:ordinary differential operator
- 適用範圍:數理科學
簡介
線性微分運算元
定義
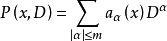

常微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。
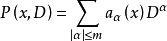

常微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...... 常微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。中文名 常微分...
在數學中,微分運算元是定義為微分運算之函式的運算元。首先在記號上,將微分考慮為一個抽象運算是有幫助的,它接受一個函式得到另一個函式(以計算機科學中高階函式的...
常係數微分運算元(differential operator with constant coefficients)是係數為常數的線性偏微分運算元。賦范向量空間E的連續自同態通常叫做有界運算元,或簡稱為運算元。 定義在...
本書論述了由線性常微分算式在空間L2上所生成的線性運算元的譜理論,本書可供高等院校數學系本科生、研究生、教師及科研人員閱讀參考。...
取英文differential,differentiation的首個字母(difference有差距,差額的意思),其中與微分概念及符號d相關的英文單詞有divide,decrease,delta等.另外,符號D又叫微分運算元...
拉普拉斯運算元(Laplace Operator)是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,...
的子集)對[0,1]區間的一個映射,我們知道實數域和[0,1]區間是可以一一映射的(這個後面再說),所以取機率符號P,我們認為也是一個運算元,和微分,積分運算元運算元沒...
概念定義 亞橢圓常係數微分運算元(hypoelliptic differen- tial operator with constant coefficients)最基本的 亞橢圓運算元.設P(D)是常係數微分運算元,則下述條 件中的...
▽ 本身並無意義,就是一個運算元,同時又被看作是一個矢量,在運算時,具有矢量和微分的雙重身份。 [2] 哈密頓運算元運算規則 編輯 ...
二階常係數線性微分方程是形如y''+py'+qy=f(x)的微分方程,其中p,q是實常數。自由項f(x)為定義在區間I上的連續函式,即y''+py'+qy=0時,稱為二階常...
在數學以及物理中,拉普拉斯運算元或是拉普拉斯算符(英語:Laplace operator, Laplacian)是由歐幾里得空間中的一個函式的梯度的散度給出的微分運算元,這名字是為了紀念法國...
向量微分運算元,Nabla運算元(nabla operator),又稱劈形運算元,倒三角運算元,是一個微分運算元。...
線性微分方程的一般形式是:其中D是微分運算元d/dx(也就是Dy = y',D2y = y...如果是常數,那么方程便稱為常係數線性微分方程。 [1] 參考資料 1. 同濟大學...
Del運算元或稱Nabla運算元,在中文中也叫向量微分運算元、劈形運算元、倒三角運算元,是一個向量微分運算元,但本身並非一個向量。...
線性微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...... 線性微分運算元是一類常見而又重要的運算元。它是微分方程中研究的核心對象。...
現代微分運算元理論是20世紀50年代,由米赫林、考爾德倫(Calderon,A.P.)和贊格蒙(Zygmund,A.)等人發展起來的奇異積分運算元理論。...
流形上微分運算元理論是流形上的分析的一個分支,它研究流形上橢圓微分運算元及擬微分運算元的阿蒂亞-辛格指標定理及其套用。...
本詞條特指在陳文燈數學複習指南中提及的解決微分方程的辦法該方法對於高速解決數學考試中的常微分方程問題效果顯著其理論來源為拉普拉斯變換...
