基本介紹
- 中文名:尤爾一沃克方程
- 外文名:Yule-Walker equation
- 相關術語:自回歸模型
- 套用:信號處理
定義,自回歸模型,
定義
尤爾·沃克公式,命名為Udny Yule和Gilbert Walker,在以下的方程組
因為只有當m = 0時,單個方程的最後部分才是非零的,所以方程組可以通過以矩陣形式表示m > 0的方程來求解,從而得到等式。

這可以為所有人解決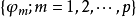 ,
, 的剩餘方程式是
的剩餘方程式是
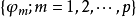

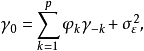
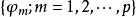

自回歸模型
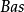



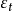
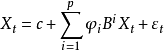


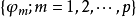

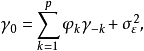
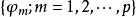

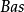



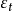
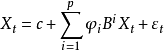
尤爾一沃克方程(Yule-Walker equation)是描述自回歸序列參數與其協方差函式之間關係的方程。在統計和信號處理中,尤爾一沃克方程與自回歸模型關係密切,是一種隨機過程...
尤爾,1871年2月18日c出生,蘇格蘭人,是一位統計學家。...... 尤爾,1871年2月18日c出生,蘇格蘭人,是一位統計...的著名的尤爾過程和尤爾—沃克方程.尤爾的研究...
1.8 尤爾沃克方程1.9 計算機實驗: 二階自回歸過程1.10 選擇模型的階數1.11 復值高斯過程1.12 功率譜密度1.13 功率譜密度的性質1.14 平穩過程通過線性濾波器傳輸...
