對數公式是數學中的一種常見公式,如果a^x=N(a>0,且a≠1),則x叫做以a為底N的對數,記做x=log(a)(N),其中a要寫於log右下。其中a叫做對數的底,N叫做真數。通常我們將以10為底的對數叫做常用對數,以e為底的對數稱為自然對數。
基本介紹
性質
基本知識





恆等式及證明
運算法則























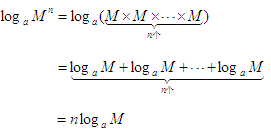 對數基本性質4推導過程
對數基本性質4推導過程







換底公式
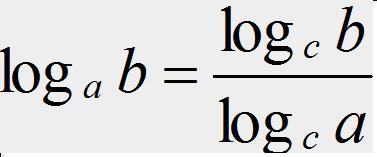


對數公式是數學中的一種常見公式,如果a^x=N(a>0,且a≠1),則x叫做以a為底N的對數,記做x=log(a)(N),其中a要寫於log右下。其中a叫做對數的底,N叫做真數。通常我們將以10為底的對數叫做常用對數,以e為底的對數稱為自然對數。




























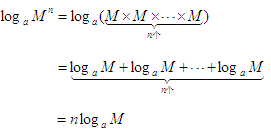 對數基本性質4推導過程
對數基本性質4推導過程







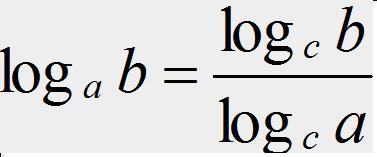

對數公式是數學中的一種常見公式,如果a^x=N(a>0,且a≠1),則x叫做以a為底N的對數,記做x=log(a)(N),其中a要寫於log右下。其中a叫做對數的底,N叫做真...
一般地,對數函式是以冪(真數)為自變數,指數為因變數,底數為常量的函式。對數函式是6類基本初等函式之一。其中對數的定義:如果ax =N(a>0,且a≠1),那么數x...
在數學中,對數是對求冪的逆運算,正如除法是乘法的倒數,反之亦然。 這意味著一個數字的對數是必須產生另一個固定數字(基數)的指數。 在簡單的情況下,乘數中的...
對數式(logarithmic expression)是一類特殊的解析式,指含有對未知數進行對數運算的解析式,如log2(x2-1),logax+b都是關於x的對數式,簡稱對數式。...
多重對數函式(polylogarithm)是一種特殊函式,通俗地講,就是使得log(i) * n ≦ 1 的最小i值。...
如果a(a>0,且a≠1)的b次冪等於N,即ab=N,那么數b叫做以a為底N的對數,記作logaN=b(其中a叫做對數的底數,N叫做真數),這就是對數變換。...
形如y=loga (x) + b的函式叫對數型函式,定義域為(0,正無窮)... 形如y=loga (x) + b的函式叫對數型函式,定義域為(0,正無窮) 形如y=loga (x) +...
如果aᵇ=n,那么log𝑎n=b。其中,a叫做“底數”,n叫做“真數”,b叫做“以a為底的n的對數”。log𝑎n函式叫做對數函式。對數函式中n的定義域是n>0,零...
被積函式當中包含有對數函式的積分公式 [5] :含有雙曲函式的積分被積函式當中包含有雙曲函式的積分公式有 [2] :積分公式定積分 定積分公式有以下幾種 [1] ...
對數留數亦稱對數殘數,是複變函數論的一個概念。如果f(z)在簡單閉曲線C上解析且不為零,在C的內部除去有限個極點以外也處處解析,那么對數留數等於簡單閉曲線C內...
對數求導法是一種求函式導數的方法。取對數的運算可將冪函式、指數函式及冪指函式運算降格成為乘法運算,可將乘法運算或除法運算降格為加法或減法運算,使求導運算...
對數似然方程(log-likelihood equation)亦簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算...
數學公式是人們在研究自然界物與物之間時發現的一些聯繫,並通過一定的方式表達出來的一種表達方法。是表征自然界不同事物之數量之間的或等或不等的聯繫,它確切的...
混合情形下,目前人們不知道如何提出一般的米爾諾公式。然而對於馴分歧這種情形,2015年,陽恩林在他的博士論文中提出了對數板米爾諾公式 [2] ,他也成功證明了這一...
阿爾奇公式是地層電阻率因素F、孔隙度ψ、含水飽和度S和地層電阻率之間的經驗關係式。阿爾奇公式是利用測井資料定量計算含油飽和度的基礎,因此儲層飽和度測井解釋模型...
DNF對數函式是DNF高手。他於2008年開始玩DNF。他最中意的角色為狂虎帝。... 一般地,如果a(a大於0,且a不等於1)的b次冪等於N,那么數b叫做以a為底N的對數,...
對數常態分配(logarithmic normal distribution)是指一個隨機變數的對數服從常態分配,則該隨機變數服從對數常態分配。對數常態分配從短期來看,與常態分配非常接近。但...
