對數似然方程(log-likelihood equation),簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算。
基本介紹
- 中文名:對數似然方程
- 外文名:log-likelihood equation
- 所屬學科:數學
- 簡稱:似然方程
- 所屬問題:統計學(估計方法)
基本概念,例題解析,
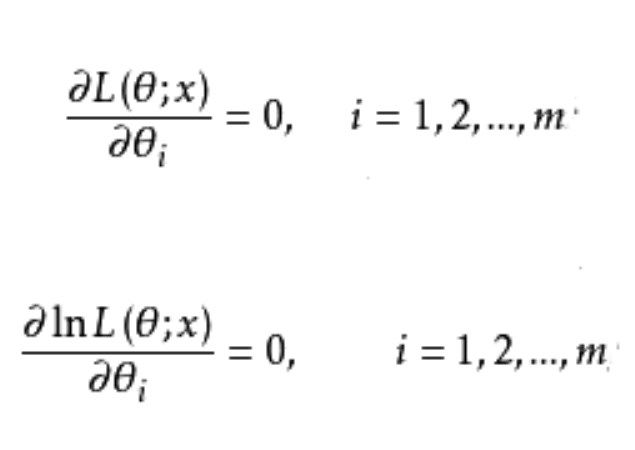
對數似然方程(log-likelihood equation),簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算。
對數似然方程(log-likelihood equation),簡稱“似然方程”。對數似然方程與原似然方程同解,由於獨立同分布的樣本的似然函式上具有連乘積,對似然方程取對數更方便計算。基本概念當總體X為連續型隨機變數時,...
此方程為對數似然方程。解對數似然方程所得,即為未知參數 的最大似然估計值。例題 設總體X~N(μ,σ²),μ,σ為未知參數,X1,X2...,Xn是來自總體X的樣本,X1,X2...,Xn是對應的樣本值,求μ與σ²的最大似然估計值。
的極大似然估計量。極大似然估計簡記為MLE或 。問題是如何把參數 的極大似然估計 求出。更多場合是利用 是 的增函式,故 與 在同一點處達到最大值,於是對似然函式 取對數,利用微分學知識轉化為求解對數似然方程 解此方程...
(1) 寫出似然函式 (2) 對似然函式取對數,並整理 (3) 求導數 (4) 解似然方程 用途 參數估計 根據從總體中抽取的樣本估計總體分布中包含的未知參數的方法。它是統計推斷的一種基本形式,是數理統計學的一個重要分支,分為點...
第4章 結構方程模型中的潛在變數選擇 4.1 引言 4.2 潛在變數選擇 4.2.1 模型介紹 4.2.2 方法 4.2.3 漸近性質 4.3 計算過程 4.3.1 極大懲罰對數似然函式的ECM算法 4.3.2 標準誤差估計 4.3.3 調節參數的...
