基本介紹
- 中文名:對偶模
- 外文名:dual module
- 適用範圍:數理科學
- 定義:對偶空間的推廣
簡介




模


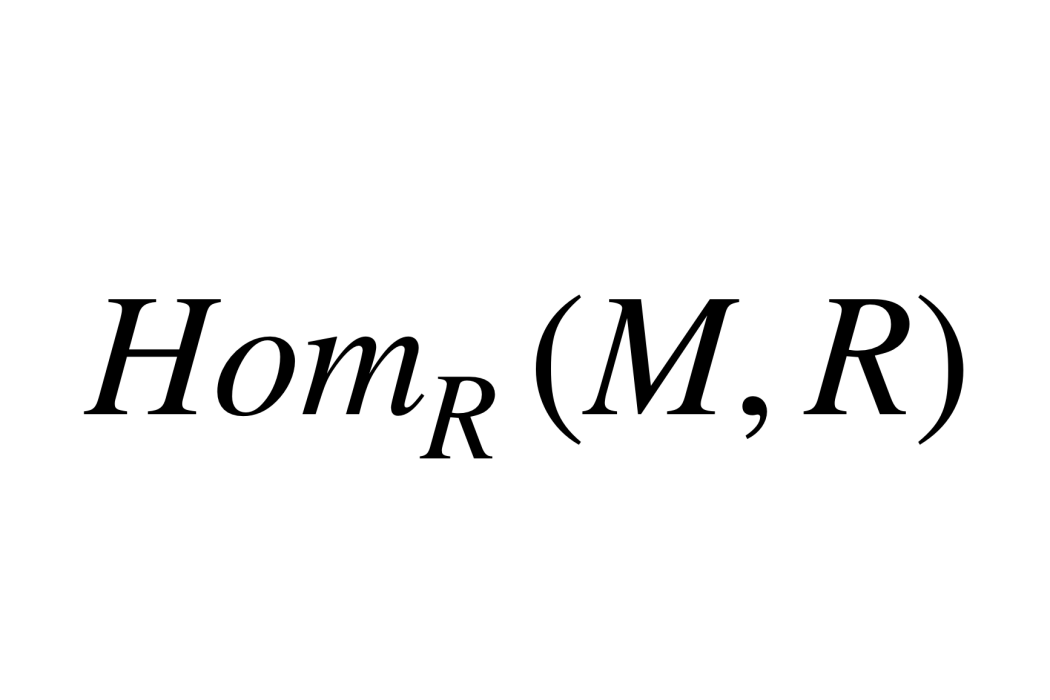






對偶模是對偶空間的推廣。在向量空間的討論中,對偶空間和雙對偶起著重要作用,而對偶模和模的雙對偶正是這兩個概念在模論中的自然推廣,它們對模的討論也有重要作用。簡介如果f:M→R 是一個模同態,我們可以在集合上定義模運算:則...
對偶範數是泛函分析中的一個概念,代表一種測度或者距離,與範數的含義一致,表示一個數。考慮一個賦范向量空間的對偶空間時,常常需要給對偶空間賦以合適的幾何架構。對偶範數是一種自然的賦范方式。定義 令 為 上的範數。對應的對偶範數,用 表示,定義為 上式含義為: 對於某一個的範數小於1的向量 , ...
U對偶函子,模範疇對偶性中的重要函子.若U是A-13雙模,則稱函子 Hom‑(一,,,U})和Hom,j(一,}Ue)為U對偶函子,且都簡記為()*=Hom(一,,,若左A模同態f : Mi-}Mz,則f* . M" }M"是右f3同態,f*‘ : Mi * }Mz‘是左A同態,稱M* _Hom‑(M,U})為M的U對偶模,f * =Hom(f,...
(1)如果G是一個連通圖且G'是G的對偶圖,則G 也是G'的對偶圖。 [4] (2)同構平面圖的對偶圖不一定是同構的。G的對偶圖的對偶圖也不一定與G同構。 (3)設n、e、f分別為平面圖G的結點數、邊數和面數, 、 、 分別為G的對偶圖 的結點數、邊數和面數.按照對偶圖的定義有 、 、 。 (4)若與G同構,...
對偶定理是一個數學術語,指的是若兩邏輯式相等,則它們的對偶式也相等。對偶式指的是對於任何一個邏輯式Y,若將其中的“·”換成“+”,“+”換成“·”,0換成1,1換成0,則得到一個新的邏輯式Y',Y'就是Y的對偶式。顯然Y和Y'互為對偶式。定義 對偶定理是揭示原始問題的解與對偶問題的解之間重要...
模範疇對偶性是數學名詞。模範疇對偶性,模範疇等價的對偶概念.設留和酬是兩個範疇,H} : }}}和H": }}}0是兩個逆變函子,若有自然等價II "II' -1、和II' II"-1_I,則稱II'與II"是對偶函子,而稱留與少是對偶範疇.模論中考慮較多的問題是:在模範疇A-Mod和Mod-13中是否有全子範疇A若和少。,...
《正則化對偶模型研究及在圖像重構中的套用》是2022年電子工業出版社出版的圖書。內容簡介 本書闡述正則化對偶模型研究及在圖像重構中的套用,主要內容包括迫近運算元基本原理,正則化對偶模型基本原理,正則化原始-對偶模型基本原理,以及迫近運算元、正則化對偶模型、正則化原始-對偶模型在圖像重構中的套用。 本書可作...
對偶原理在現代數學特別是幾何學、代數學、拓撲學等學科中有著廣泛的套用,對於推動數學的發展起著很好的作用。舉例來講,在範疇論中,藉助於對偶變換(對偶化),由始對象便可得終對象、由單態射得滿態射、由核得上核、由積得上積;在同調代數中,由正向極限得反向極限、由內射模得投射模、由內射包得投射包、由...
對偶擬陣(dual matroid)亦稱正交擬陣,是一種組合構形,它是由擬陣M導出的擬陣M*,當擬陣M以基集族B表示時,M=(E,B),則M*=(E,B*),其中B*={E-B:B∈B}。因此,當B為擬陣M的基時,E-B就是對偶擬陣的基,對於擬陣而言,其對偶擬陣總存在,而且M**=(M*)*=M,如此完整的對稱性是擬陣特有的...
《對偶三角模-三角余模邏輯及推理》是2015年科學出版社出版的圖書,作者是張興芳。內容簡介 本書總結作者張興芳2005年以來關於機率論、Lawry的適當測度理論、劉寶碇的不確定理論、模糊集理論與數理邏輯理論的結合研究成果。根據非經典命題和謂詞的不確定性的各種特徵,作者分別提出了相應的邏輯和推理方法,概括其本質分別...
《模範疇的對偶》是依託福建師範大學,由薛衛民擔任項目負責人的面上項目。項目摘要 該項目研究結合環上的模範疇的對偶,利用模的線性緊性、內射性、及環的擴張性質研究環和模的結構和性質。刻劃了具有Morita對偶的Artin環,包括OF環和Seriat環,探討環擴張和對偶,在Morita對偶中研究L-內射模等特殊模,用線性緊性...
對偶環是森田紀一(Morita , K.)於1958年首先提出並研究的.它是半完全環(奧索夫茨克(Osofsky, B. I_.,1966年)證明的),並且交換對偶環是局部環的有限直和.繆勒(Muller , B. J.)證明:環R是對偶環若且唯若*R和左R模範疇的極小餘生成子都是線性緊緻的且對於對偶環,線性緊緻模和反射模是等價的.
在數學裡,任何向量空間V都有其對應的對偶向量空間(或簡稱為對偶空間),由V的線性泛函組成。此對偶空間具有一般向量空間的結構,像是向量加法及標量乘法。由此定義的對偶空間也可稱之為代數對偶空間。在拓撲向量空間的情況下,由連續的線性泛函組成的對偶空間則稱之為連續對偶空間。對偶空間是行向量(1×n)與列...
若G是局部緊緻阿貝爾群,G的特徵標是一個從G到圓群T的連續群同態;特徵標在逐點乘法下構成一個群,一個特徵標的逆元是它的復共軛。可證明所有G上的特徵標在緊緻開拓撲(即:以緊集上的一致收斂定義收斂性)下構成一個局部緊緻阿貝爾群,稱作對偶群。定義 若 是局部緊緻阿貝爾群, 的特徵標是一個從 到圓...
63大類修辭手法分別是:比喻, 白描,比擬(又名比體,分為擬人、擬物),避復,變用,層遞,襯墊(襯跌) ,襯托(反襯、陪襯),倒文,倒裝,迭音,疊字復疊,頂真(又名頂針、聯珠),對比,對偶(對仗、排偶),翻新,反覆,反問,反語,仿詞,仿化,飛白,分承(並提、合敘、合說);復迭錯綜,複合偏義...
獲得的結論對領域內的這一公開問題給出了正面的回答,同時將國際上構造對偶余模的方法首次予以了統一,揭示了對偶余模本性,為同調余代數、余代數K理論的建立打下了基石。這些結果為國內外學者多次引用,被認為是余代數K理論方面最深刻的理論成果。另外,郝志峰還發現了對偶余模結構的外部的余模、余代數的表征,第一...
餘一致模 餘一致模(co-uniform module)一致模的對偶概念.設M是A模,若M的每個真子模在M中是多餘子模,則稱M是餘一致模.M是餘一致模的充分必要條件是,投射模P是不可分解的,這裡p:P->M是M的投射覆蓋.
