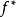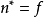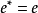對偶圖是與平面圖相伴的一種圖。對於給定平面圖G=〈V,E〉,設G的面為F1,F2,…,Fe,當圖G*滿足如下條件時,則圖G*=〈V*,E*〉稱為G的對偶圖:
①對G的每個面Fo,內部任選一點v*o∈V*;
②對Fo,Fx的每一條公共邊界eə,vo*與vx*間有一條邊eə*,並且eə*與eə交於一點;
③若且唯若eə僅是一個面Fo的邊界時,vo*有一個環(自迴路),eo*與eə相交。
基本介紹
- 中文名:對偶圖
- 外文名:dual graph
- 屬性:圖論里的概念
- 所屬學科:數學
- 相關概念:連通圖
概念,構造方法,性質,
概念
設G是平面圖,在圖G的每個面中指定一個新結點,對兩個面公共的邊,指定一條新邊與其相交。由這些新結點和新邊組成的圖稱為G的對偶圖 。
。

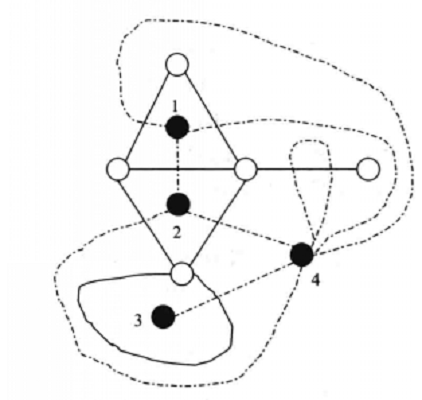
例1 圖1的圖(b)中的虛線是圖(a)的對偶圖。
 圖1
圖1例2 圖2的圖(b)中的虛線是圖(a)的對偶圖。
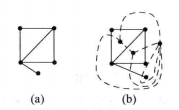 圖2
圖2構造方法
給定平面圖G,用如下的方法構造G的對偶圖 :
:

2)若 是G的兩個面
是G的兩個面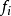 和
和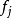 的公共邊.有一條邊
的公共邊.有一條邊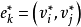 作為
作為 的邊,且
的邊,且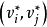 與
與 相交;
相交;

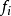
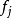
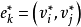

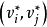

性質
(1)如果G是一個連通圖且G'是G的對偶圖,則G 也是G'的對偶圖。
(2)同構平面圖的對偶圖不一定是同構的。G的對偶圖的對偶圖也不一定與G同構。
(4)若與G同構,稱G自對偶(self dual)。
(5)任何平面圖G的對偶圖都是連通的。
(6)若邊e為G中的環,則它對應的邊為的割邊;若邊e為G中的割邊,則為的環;
(7)G存在唯一的對偶圖;
如圖3、4所示圖G,以虛線為邊的圖即為G的對偶圖。
 圖3
圖3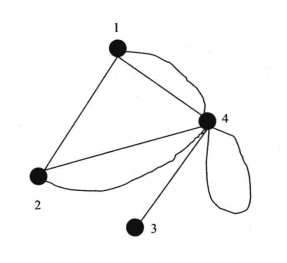 圖4
圖4