基本介紹
- 中文名：定量構效關係
- 外文名：Quantitative Structure - Activity Relationship
- 英文縮寫：Acronym
- 基礎：傳統構效關係
中英文名稱,Hansch方法,二維定量構效關係,活性參數,結構參數,數學模型,Hansch方程形式,發展,三維定量構效關係,CoMFA&CoMSIA,CoMFA結果輸出,三維定量構效,方法評價,
中英文名稱
英文縮寫 (Acronym):
QSAR
中文全稱 (Chinese):
定量構效關係
英文全稱(English):
Quantitative Structure - Activity Relationship
中文意思 (Chinese Introduction):
無
英文介紹 (English Explanation):
None
發展歷史
定量構效關係是在傳統構效關係的基礎上，結合物理化學中常用的經驗方程的數學方法出現的，其理論歷史可以追溯到1868年提出的Crum-Brown方程，該方程認為化合物的生理活性可以用化學結構的函式來表示，但是並未建立明確的函式模型。最早的可以實施的定量構效關係方法是美國波蒙拿學院的Hansch在1962年提出的Hansch方程。Hansch方程脫胎於1935年英國物理化學家哈密頓提出的哈密頓方程以及改進的塔夫托方程。哈密頓方程是一個計算取代苯甲酸解離常數的經驗方程，這個方程將取代苯甲酸解離常數的對數值與取代基團的電性參數建立了線性關係，塔夫托方程是在哈密頓方程的基礎上改進形成的計算脂肪族酯類化合物水解反應速率常數的經驗方程，它將速率常數的對數與電性參數和立體參數建立了線性關係。
Hansch方程在形式上與哈密頓方程和塔夫托方程非常接近，以生理活性物質的半數有效量作為活性參數，以分子的電性參數、立體參數和疏水參數作為線性回歸分析的變數，隨後，Hansch和日本訪問學者藤田稔夫等人一道改進了Hansch方程的數學模型，引入了指示變數、拋物線模型和雙線性模型等修正，使得方程的預測能力有所提高。
Hansch方法
幾乎在Hansch方法發表的同時，Free等人發表了Free-Wilson方法，這種方法直接以分子結構作為變數對生理活性進行回歸分析。其在藥物化學中的套用範圍遠不如Hansch方法廣泛。Hansch方法、Free-Wilson方法等方法均是將分子作為一個整體考慮其性質，並不能細緻地反應分子的三維結構與生理活性之間的關係，因而又被稱作二維定量構效關係
二維定量構效關係出現之後，在藥物化學領域產生了很大影響，人們對構效關係的認識從傳統的定性水平上升到定量水平。定量的結構活性關係也在一定程度上揭示了藥物分子與生物大分子結合的模式。在Hansch方法的指導下，人們成功地設計了諾氟沙星等喹諾酮類抗菌藥。
由於二維定量不能精確描述分子三維結構與生理活性之間的關係，1980年代前後人們開始探討基於分子構象的三維定量構效關係的可行性。1979年，Crippen提出“距離幾何學的3D-QSAR”；1980年Hopfinger等人提出“分子形狀分析方法”；1988年Cramer等人提出了“比較分子場方法”（CoMFA）。比較分子場方法一經提出便席捲藥物設計領域，成為套用最廣泛的基於定量構效關係的藥物設計方法；1990年代，又出現了在比較分子場方法基礎上改進的“比較分子相似性方法”以及在“距離幾何學的3D-QSAR”基礎上發展的“虛擬受體方法”等新的三維定量構效關係方法，但是老牌的CoMFA依然是使用最廣泛的定量構效關係方法。
二維定量構效關係
二維定量構效關係方法是將分子整體的結構性質作為參數，對分子生理活性進行回歸分析，建立化學結構與生理活性相關性模型的一種藥物設計方法，常見的二維定量構效關係方法有Hansch方法、Free-wilson方法、分子連線性方法等，最為著名和套用最廣泛的是Hansch方法
活性參數
活性參數是構成二維定量構效關係的要素之一，人們根據研究的體系選擇不同的活性參數，常見的活性參數有：半數有效量、半數有效濃度、半數抑菌濃度、半數致死量、最小抑菌濃度等，所有活性參數均必須採用物質的量作為計量單位，以便消除分子量的影響，從而真實地反應分子水平的生理活性。為了獲得較好的數學模型，活性參數在二維定量構效關係中一般取負對數後進行統計分析。
結構參數
結構參數是構成定量構效關係的另一大要素，常見的結構參數有：疏水參數、電性參數、立體參數、幾何參數、拓撲參數、理化性質參數以及純粹的結構參數等
* 疏水參數：藥物在體內吸收和分布的過程與其疏水性密切相關，因而疏水性是影響藥物生理活性的一個重要性質，在二維定量構效關係中採用的疏水參數最常見的是脂水分配係數，其定義為分子在正辛醇與水中分配的比例，對於分子母環上的取代基，脂水分配係數的對數值具有加和性，可以通過簡單的代數計算獲得某一取代結構的疏水參數。
* 電性參數：二維定量構效關係中的電性參數直接繼承了哈密頓公式和塔夫托公式中的電性參數的定義，用以表征取代基團對分子整體電子分配的影響，其數值對於取代基也具有加和性。
* 幾何參數：幾何參數是與分子構象相關的立體參數，因為這類參數常常在定量構效關係中占據一定地位，故而將其與立體參數分割考慮，常見的幾何參數有分子表面積、溶劑可及化表面積、分子體積、多維立體參數等
* 拓撲參數：在分子連線性方法中使用的結構參數，拓撲參數根據分子的拓撲結構將各個原子編碼，用形成的代碼來表征分子結構。
* 純粹的結構參數：在Free-Wilson方法中，使用純粹的結構參數，這種參數以某一特定結構的分子為參考標準，依照結構母環上功能基團的有無對分子結構進行編碼，進行回歸分析，為每一個功能基團計算出回歸係數，從而獲得定量構效關係模型。
數學模型
Hansch方程形式
日本學者藤田稔夫對經典的Hansch方程作出一定改進，用拋物線模型描述疏水性與活性的關係：
lg \left(\frac{1}{C}\right)=a\pi+b{\pi}^2+c\sigma+dE_s+k這一模型擬合效果更好。
Hansch方程進一步，以雙直線模型描述疏水性與活性的關係：
lg \left(\frac{1}{C}\right)=algP-blg(\beta P+1)+D其中的P為分子的脂水分配係數，a,b,β為回歸係數，D代表方程的其他部分。雙直線模型的預測能力比拋物線模型進一步加強。
Free-Wilson方法的方程形式為：
lg \left(\frac{1}{C}\right)=\sum_i\sum_jG_{ij}X_{ij}+\mu其中Xij為結構參數，若結構母環中第i個位置有第j類取代基則結構參數取值為1否則為0，μ為參照分子的活性參數，Gij為回歸係數。
除了回歸分析，遺傳算法、人工神經網路、偏最小二乘分析、模式識別、單純形方法等統計分析方法也會套用於二維定量構效關係數學模型的建立
發展
目前，二維定量構效關係的研究集中在兩個方向：結構數據的改良和統計方法的最佳化。
三維定量構效關係
三維定量構效關係是引入了藥物分子三維結構信息進行定量構效關係研究的方法，這種方法間接地反映了藥物分子與大分子相互作用過程中兩者之間的非鍵相互作用特徵，相對於二維定量構效關係有更加明確的物理意義和更豐富的信息量，因而1980年代以來，三維定量構效關係逐漸取代了二維定量構效關係的地位，成為基於機理的合理藥物設計的主要方法之一。目前套用最廣泛的三維定量構效關係方法是CoMFA 和CoMSIA即比較分子場方法和比較分子相似性方法，除了上述兩種方法，3D-QSAR還有DG 3D-QSAR、MSA、GERM等眾多方法。
CoMFA&CoMSIA
CoMFA和CoMSIA是套用最廣泛的合理藥物設計方法之一，這種方法認為，藥物分子與受體間的相互作用取決於化合物周圍分子場的差別，以定量化的分子場參數作為變數，對藥物活性進行回歸分析便可以反應藥物與生物大分子之間的相互作用模式進而有選擇地設計新藥。
分子定位在一個方格中，作為探針的粒子在盒子中遊走
比較分子場方法將具有相同結構母環的分子在空間中疊合，使其空間取向儘量一致，然後用一個探針粒子在分子周圍的空間中遊走，計算探針粒子與分子之間的相互作用，並記錄下空間不同坐標中相互作用的能量值，從而獲得分子場數據。不同的探針粒子可以探測分子周圍不同性質的分子場，甲烷分子作為探針可以探測立體場，水分子作為探針可以探測疏水場，氫離子作為探針可以探測靜電場等等，一些成熟的比較分子場程式可以提供數十種探針粒子供用戶選擇。
探針粒子探測得到的大量分子場信息作為自變數參與對分子生理活性數據的回歸分析，由於分子場信息數據量很大，屬於高維化學數據，因而在回歸分析過程中必須採取數據降維措施，最常用的方式是偏最小二乘回歸，此外主成分分析也用於數據的分析。
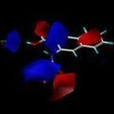
CoMFA結果輸出
統計分析的結果可以圖形化地輸出在分子表面，用以提示研究者如何有選擇地對先導化合物進行結構改造。右圖為一CoMFIA計算的結果輸出，圖中藍色區域若以負電性基團取代則會提高藥物的活性，紅色區域則提示正電性基團更有利於活性。除了直觀的圖形化結果，CoMFA還能獲得回歸方程，以定量描述分子場與活性的關係。
CoMSIA是對CoMFA方法的改進，他改變了探針粒子與藥物分子相互作用能量的計算公式，從而獲得更好的分子場參數。
三維定量構效
除了比較分子場方法，三維定量構效關係還有距離幾何學三位定量構效關係(DG 3D-QSAR)、分子形狀分析(MSA)、虛擬受體等方法(FR)等
距離幾何學三維定量構效關係嚴格來講是一種介於二維和三維之間的QSAR方法。這種方法將藥物分子劃分為若干功能區塊定義藥物分子活性位點，計算低能構象時各個活性位點之間的距離，形成距離矩陣；同時定義受體分子的結合位點，獲得結合位點的距離矩陣，通過活性位點和結合位點的匹配為每個分子生成結構參數，對生理活性數據進行統計分析。
分子形狀分析認為藥物分子的藥效構象是決定藥物活性的關鍵，比較作用機理相同的藥物分子的形狀，以各分子間重疊體積等數據作為結構參數進行統計分析獲得構效關係模型。
虛擬受體方法是DG 3D-QSAR和CoMFA方法的延伸與發展，其基本思路是採用多種探針粒子在藥物分子周圍建立一個虛擬的受體環境，以此研究不同藥物分子之間活性與結構的相關性。其原理較之CoMFA方法更加合理，是目前定量構效關係研究的熱點之一。
方法評價
定量構效關係研究是人類最早的合理藥物設計方法之一，具有計算量小，預測能力好等優點。在受體結構未知的情況下，定量構效關係方法是最準確和有效地進行藥物設計的方法，根據QSAR計算結果的指導藥物化學家可以更有目的性地對生理活性物質進行結構改造。在1980年代計算機技術爆炸式發展之前，QSAR是套用最廣泛也幾乎是唯一的合理藥物設計手段。
