基本介紹
- 中文名:基礎矩陣
- 外文名:Fundamental matrix
- 形式:3×3的矩陣
- 表達:立體像對的像點之間的對應關係
- 學科:計算機視覺
- 領域:計算機視覺
簡介



推導

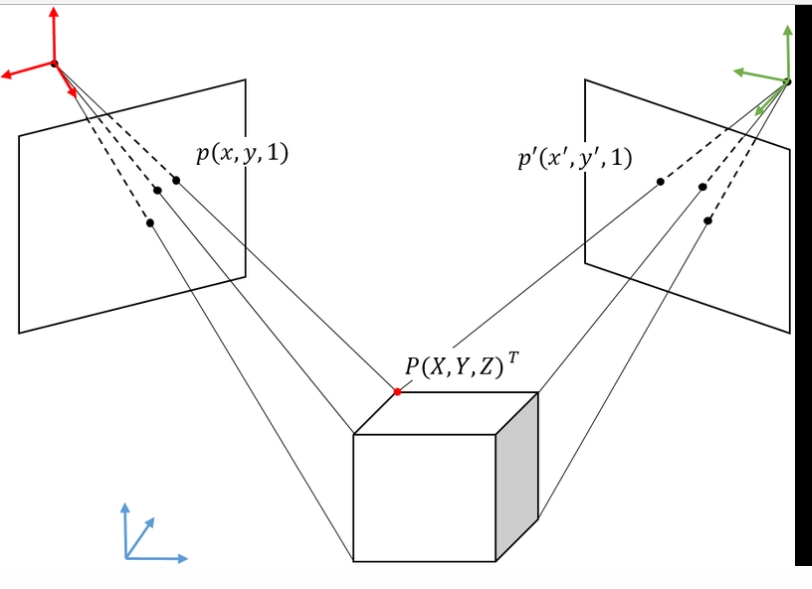




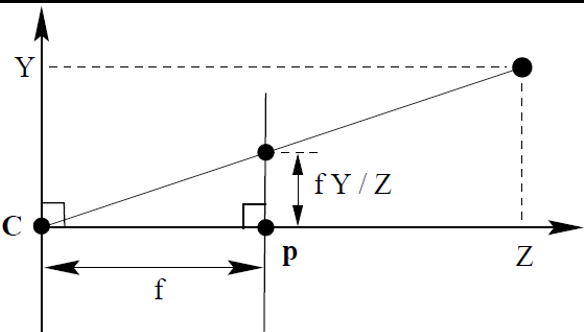
















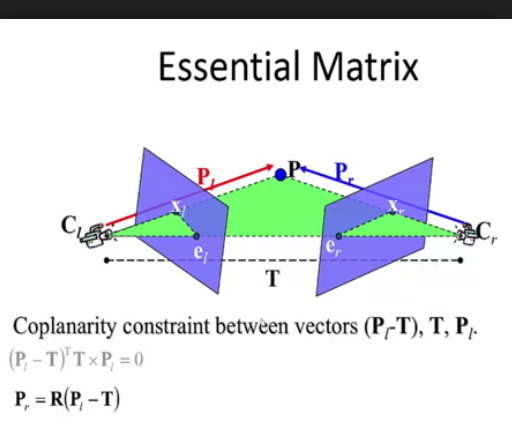


























在計算機視覺中,基礎矩陣(Fundamental matrix)F是一個3×3的矩陣,表達了立體像對的像點之間的對應關係。簡介在計算機視覺中,基礎矩陣(Fundamental matrix)F是一個3×3的矩陣,表達了立...
現在我們用矩陣形式寫出基向量和基,這樣的矩陣我們叫它基矩陣。空間坐標系的基和基矩陣 在3-D空間中,我們用空間坐標系來規範物體的位置,空間坐標系由3個相互垂直的坐標軸組成,我們就把它們作為我們觀察3-D空間的基礎,空間中物體的...
《矩陣基本理論與套用》是2021年北京航空航天大學出版社出版的圖書,作者是王磊。內容簡介 本書共分五章,較全面系統地介紹了矩陣的基本理論、方法和典型套用。第1、2章是線性代 數的基礎理論,主要介紹線性空間與內積空間、線性映射與線性...
著作權的高清電影電視打下基礎 包交換型原理 包交換型虛擬矩陣器是通過包交換的方式(通常是IP包)實現圖像數據的傳輸和切換。包交換型矩陣目前已經比較普及,比如已經廣泛套用的遠程監控中心,即在本地錄像端把圖像壓縮,然後把壓縮的碼流通過...
在複雜的質量問題中,往往存在許多成對的質量因素,將這些成對因素找出來,分別排列成行和列,其交點就是其相互關聯的程度,在此基礎上再找出存在的問題及問題的形態,從而找到解決問題的思路。簡介 矩陣圖法(Matrix Diagram)矩陣圖的...
一般單指矩陣乘積時,指的便是一般矩陣乘積。一個m×n的矩陣就是m×n個數排成m行n列的一個數陣。由於它把許多數據緊湊地集中到了一起,所以有時候可以簡便地表示一些複雜的模型,如電力系統網路模型。定義 設 A 為 的矩陣,B ...
矩陣變換是線性代數中矩陣的一種運算形式。線上性代數中,矩陣的初等行變換是指以下三種變換類型 :(1) 交換矩陣的兩行(對調i,j,兩行記為ri,rj);(2) 以一個非零數k乘矩陣的某一行所有元素(第i行乘以k記為ri×k);(3...
描述最輕的三種夸克時,需要用到一種內含特殊酉群SU(3)的群論表示;物理學家在計算時會用一種更簡便的矩陣表示,叫蓋爾曼矩陣,這種矩陣也被用作SU(3)規範群,而強核力的現代描述──量子色動力學的基礎正是SU(3)。還有卡比博-...
Gell-Mann矩陣實際就是上是SU(3)群特定選取的一組生成元(李代數)的特定基礎表示。所謂“特定選取”是指這些矩陣的正交性(至多差一個歸一化因子)。也就是說以這些特定矩陣為基的SU(3)伴隨表示是么正的。“特定基礎表示”是由於...
拉普拉斯矩陣(Laplacian matrix) 也叫做導納矩陣、基爾霍夫矩陣或離散拉普拉斯運算元,主要套用在圖論中,作為一個圖的矩陣表示。定義 給定一個有 個頂點的圖 ,它的拉普拉斯矩陣 定義為:其中 為圖的度矩陣,為圖的鄰接矩陣。度矩陣在有...
在矩陣圖的基礎上,把各個因素分別放在行和列,然後在行和列的交叉點中用數量來描述這些因素之間的對比,再進行數量計算,定量分析,確定哪些因素相對比較重要的。套用時機 當我們進行顧客調查、產品設計或者其他各種方案選擇,做決策的時候...
模擬矩陣的方案還需要視頻信號的分配、復用設備來實現DVR的錄像功能,而採用數字矩陣,則只需在DVR的基礎之上,增加簡單的矩陣模組即可,成本相對低廉,且數字矩陣、錄像系統的集成度高,穩定性增強,也降低了以後維護的成本。功能 配置靈活...
競爭情報領域用此方法來發現競爭對手,現用安索夫矩陣為基礎來分析高校圖書館所面臨的競爭對手和競爭局勢。 發現高校圖書館競爭對手的安索夫矩陣: 由安索夫矩陣可以看出高校圖書館所面臨的不同層次的競爭,分別對各層次競爭者進行分析: D類...
零階相關矩陣 零階相關矩陣,即泊松相關矩陣,是指以X{x1,x2,...,xn}為列,Y{y1,y2,...,yn}為行,排列成rij的矩陣,若符合關係R,則顯示為1,否則為0。以此判斷X,Y的關係為基礎的矩陣。
矩陣制是由職能部門系列和為完成某一臨時任務而組建的項目小組系列組成,它的最大特點在於具有雙道命令系統。矩陣制組織形式是在直線職能制垂直形態組織系統的基礎上,再增加一種橫向的領導系統,可稱之為“非長期固定性組織”。矩陣制的...
矩陣型組織結構的基礎的、核心的技術資源可供所有項目運用,從而提高公司整體上的技術資源利用能力。同一職能部門的專業人員具有共同的知識背景,可以相互交流與學習,共同得到提高。他們將自己的知識套用於各個不同的項目,各職能部門的員工...
矩陣理論和代數基礎 《矩陣理論和代數基礎》是1989年電子科技大學出版社出版的圖書,作者是李正良。
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數,通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數目。類似地,行秩是A的線性無關的...
TR,線性代數中的數學概念符號,意為跡/跡數。一個矩陣的跡是其特徵值的總和(按代數重數計算)。對於矩陣A,設A=(aij)是一個n階方陣,A的對角線元素之和稱為A的跡,記為trA,即trA=a11+a22+...+ann。跡的英文為trace,是...
