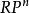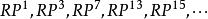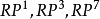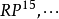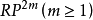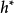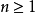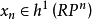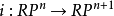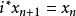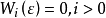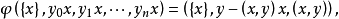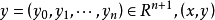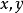基本介紹
- 中文名:史梯福-惠特尼類
- 外文名:Stiefel-Whitney class
- 所屬學科:數學
- 所屬領域:代數拓撲學
- 相關概念:正交群、示性類、線叢等
基本介紹,史梯福-惠特尼類的性質,
基本介紹
1.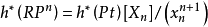 ;
;
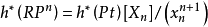
則對於以 復形
復形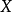 為底空間的每個
為底空間的每個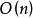 叢ξ,存在惟一的
叢ξ,存在惟一的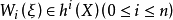 滿足:
滿足:

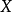
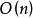
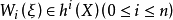
1.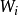 (
(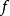 #ξ)
#ξ)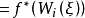 ,對於一切
,對於一切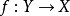 ;
;
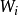
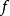
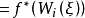
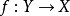
2.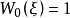 ;
;
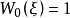
3.若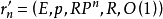 為
為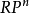 上的典型線叢,則
上的典型線叢,則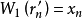 ;
;
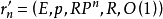
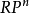
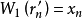
4.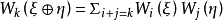 。
。
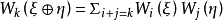
由於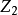 係數的奇異上同調
係數的奇異上同調 滿足定理中的條件1,2,因此,對於
滿足定理中的條件1,2,因此,對於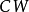 復形X上的每個
復形X上的每個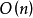 叢ξ,存在惟一的
叢ξ,存在惟一的
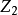

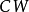
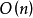
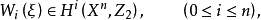
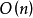
史梯福-惠特尼類的性質
史梯福-惠特尼類的性質(properties of Stiefel-Whitney classes)是對史梯福-惠特尼類的刻畫,指它的一些基本性質。即:
1.若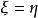 ,則
,則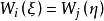 。
。
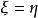
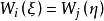
3.若ε為平凡叢,則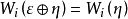 。
。
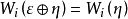
4.若向量叢ξ有k個獨立的截面,則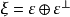 ,其中ε為k維平凡叢,從而
,其中ε為k維平凡叢,從而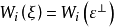 ,所以
,所以
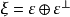
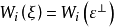

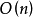
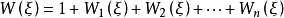
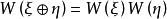
5.設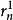 為
為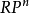 上的典型線叢,則
上的典型線叢,則
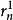
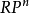
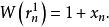
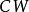
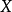
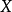
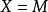
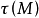
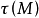
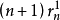
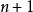
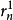
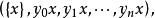
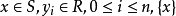
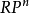
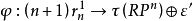
6.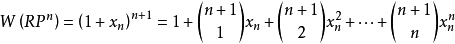 。
。
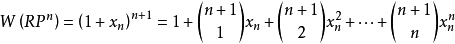
由於這個性質6與性質4,即得下列性質(史梯福的一個定理):
7.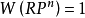 ,若且唯若
,若且唯若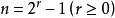 。
。
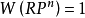
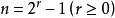
因此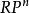 可平行化(即它的切叢為平凡叢),僅可能是
可平行化(即它的切叢為平凡叢),僅可能是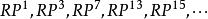 事實上,已經知道
事實上,已經知道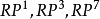 可以平行化,而
可以平行化,而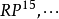 不能平行化。此外,由性質4與6還可知:
不能平行化。此外,由性質4與6還可知: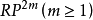 上沒有截面,即,沒有連續處處非零的向量場。
上沒有截面,即,沒有連續處處非零的向量場。