基本介紹
- 中文名:上同調環
- 外文名:cohomology ring
- 領域:數學
- 性質:環結構
- 空間:拓撲空間
- 環:交換環
簡介
定義

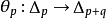



環


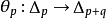




環是對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則...
上同調維數是群的不變數,量度群的表示的同調複雜度。上同調維數在幾何群論、拓撲學、代數數論中有重要套用。...
模論是抽象代數學的重要組成部分之一,主要研究環上的模。模的概念本質上是域上向量空間的直接推廣。早在19世紀,狄利克雷(Dirichlet,P.G.L.)就曾經考慮過多項式...
上同調運算(cohomology operations)作用在上同調群上的一種自然變換,它是代數拓撲學中的一個重要工具。在同調論中,上同調是對一個在上鏈復形(co-chain)上定義一...
3奇異上同調中的乘法 3.1奇異上鏈的上積與卡積 3.2在上同調的水平上,上積與卡積的基本性質 3.3分次環與分次模,上同調環與下同調模 3.4上同調環的交換...
德拉姆上同調(de Rham cohomology) 是同時屬於代數拓撲和微分拓撲的工具。它能夠以一種特別適合計算和用具體的上同調類的方式表達關於光滑流形的基本拓撲信息。它是...
在緊多面體的情況,這兩種同調群都同構於按單純剖分得到的同調群。在以某種環為係數的上同調群中可以引入乘法使之成為上同調環。為了更好地利用上同調群,在其上...
同調流形(homology manifold)是一類重要的拓撲空間。設(X,A)為拓撲空間偶,若...旗流形的上同調環的自同態[J]. 數學學報,2001,(06):1099-1106. [2017-10...
阮勇斌教授,在辛拓撲與量子上同調等方面的開創性研究在國際數學界有重要影響。基於其出色的工作,他獲得了美國Sloan研究基金,並且被邀請在1998年的國際數學家大會上做...
中的一項重要工具.周煒良環在許多情形可以代替上同調環.在證明各種黎曼-羅赫定理時,常用周煒良環去導出陳省身類.著名的韋伊(Weil)猜想的解決,也可使用周煒良環....
李安民與阮勇斌合作,提出並建立了相對GW不變數理論,證明了辛切割下的粘合公式,給出了Witten穿牆公式的數學證明,證明了兩個3維光滑極小模型有同構的量子上同調環。與...
與阮勇斌合作,提出並建立了相對GW不變數理論,證明了辛切割下的粘合公式,給出了Witten穿牆公式的數學證明,證明了兩個3維光滑極小模型有同構的量子上同調環。與人...
全書共分8章74節,內容豐富,論述精闢,主要內容包括單純同調群及其拓撲不變性、Eilenberg-Steenrod公理系統、奇異同調論、上同調群與上同調環、同調代數、流形上的...
1936年發表的論文中,柯爾莫哥洛夫定義了任一局部緊緻拓撲空間的上同調群的概念。1935年,在莫斯科國際拓撲學會議上,柯爾莫哥洛夫定義了上同調環。...
50年代前夕,懷特海證明:當n>2時,A2n多面體的倫型與A2n上同調系統的正則同構類一一對應;又於n=2時,A22多面體的倫型與A22上同調環的正則同構類一一對應。這就...
江澤涵,孫以豐. 球上纖維叢的同調群. 數學學報,1951,1: 247-256.江澤涵,周毓麟,賀錫章. 球上線素的流形的上同調環. 北京大學學報(自然科學版),1956(2)...
映到0。因此,V 不是其上同調代數的模型。它們各自對應的拓撲空間因而擁有相同的有理上同調環而相異的有理同倫型。注意到 是Massey積 中的元素。參考...
不說他老人家在數學上的成就了,因為實在太多,譬如說上同調環這個東西他也是獨立發現的。專心的說一下他的軼事。Kolmogorov總是以感激的口氣提到史達林:“首先,他在...
