卡拉西奧多里條件是用以定義勒貝格可測集的一個條件。這一條件是卡拉西奧多里(Caratheodory,C.)於1914年首先提出的,它在非線性積分運算元理論和各種非線性問題中,起著重要的作用。
基本介紹
- 中文名:卡拉西奧多里條件
- 外文名:Caratheodory condition
- 適用範圍:數理科學
簡介
發展
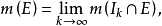

卡拉西奧多里條件是用以定義勒貝格可測集的一個條件。這一條件是卡拉西奧多里(Caratheodory,C.)於1914年首先提出的,它在非線性積分運算元理論和各種非線性問題中,起著重要的作用。
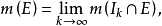

卡拉西奧多里條件是用以定義勒貝格可測集的一個條件。這一條件是卡拉西奧多里(Caratheodory,C.)於1914年首先提出的,它在非線性積分運算元理論和各種非線性問題中,起...
卡拉西奧多里(Caratheodory,Constantin 1873~1950)希臘裔數學家。...... 卡拉西奧多里(Caratheodory,Constantin 1873~1950)希臘裔數學家。中文名 卡拉西奧多里 外文名...
卡拉西奧多里定理(Caratheodory theorem )有限維凸集的表示定理.該定理斷言,n維空間中的凸集中的每一點都可用該集合的不超過n+l個點的凸組合來表示。...
卡拉西奧多里度量是由全純映射集合誘導的一種度量。全純映射是複流形之間的解析映射。...
卡拉西奧多里偽距是距離的定義方式之一。在數學中,距離是泛函分析中最基本的概念之一。...
卡拉西奧多里-哈恩延拓定理是關於測度延拓的重要結果。數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等...
G的素端的全體稱為G的卡拉西奧多里邊界,簡稱卡氏邊界。早在1913年,卡拉西奧多里(Carathéodory,C.)就已證明單連通區域間的共形映射可同胚開拓到卡氏邊界。...
卡拉西奧多里,C. 數學家。希臘族人。1873年9月13日生於柏林,1950年2月2日卒於慕尼黑。1875年隨父到比利時,1891~1895年在比利時軍事學校學習。畢業後被英政府...
卡拉西奧多里在深入研究了勒貝格外測度理論後,於1914年指出:若μ*是Rn上的勒貝格外測度,則 是集A⊂Rn勒貝格可測的充分必要條件。這個條件比較簡潔,同時又易於...
若m*為Rn上的(L)外測度,E⊂Rn且滿足卡拉西奧多里條件,即對任意點集T⊂Rn,有:則集E稱為勒貝格可測集,簡稱(L)可測集。但這不是勒貝格(Lebesgue,H.L....
若m*為Rn上的(L)外測度,E⊂Rn且滿足卡拉西奧多條件,即對任意點集T⊂Rn,有 則稱集E為勒貝格可測集,簡稱(L)可測集。勒貝格可測集點集的可測集 編輯 ...
卡拉西奧多里證明了邊界對應定理,即在黎曼映射定理的條件下 ,若бD= L是一條簡單閉曲線,則映射函式f(Z) 可以連續開拓到L上且實現L與|w|=1之間的雙方單值...
若f是可測空間(Ω,F)上的實值函式,則f在(Ω,F)上可測的充分必要條件是f...卡拉西奧多里(C.Carathéodory)於1914年發展了外測度理論,對測度進行了公理化研究...
經過C.卡拉西奧多里、E.G.H.蘭道、蒙泰爾及A.奧斯特羅夫斯基的工作,亞純函式正規族的理論也建立起來。如果一致收斂性是用球面距離來定義,那么亞純函式正規族的...
設G是RN中的可測集,m(G)≠0,若f(x,u)滿足卡拉西奧多里條件,則運算元fφ=f(x,φ(x))稱為涅梅茨基運算元。涅梅茨基運算元性質 編輯 涅梅茨基運算元將可測...
對於任意一個滿足條件的圖形,都可以先縮小,找到中點後擴大,這樣一定有一異於原點的整點在圖形內,命題得證。閔可夫斯基定理套用 編輯 閔可夫斯基定理是卡拉西奧多里...
這個條件稱為柯西-黎曼方程。在域D內可導的函式稱為解析函式或全純函式。由...後來C·卡拉西奧多里進一步指出,在黎曼映射定理中,若域D的邊界為一簡單閉曲線C...
康斯坦丁·卡拉西奧多里在1912年發表了第一個完整證明。該定理是複變函數幾何理論最基本、最重要的定理,是幾何函式論的基礎黎曼映射定理定理 編輯 ...
