涅梅茨基運算元

涅梅茨基運算元是在非線性微分方程和非線性積分方程的研究中起重要作用的一類非線性運算元。這一類運算元，是涅梅茨基在1934年首先提出並加以研究的。

基本介紹

• 中文名：涅梅茨基運算元
• 外文名：Remesky operator
• 適用範圍：數理科學

簡介

涅梅茨基運算元是在非線性微分方程和非線性積分方程的研究中起重要作用的一類非線性運算元。這一類運算元，是涅梅茨基在1934年首先提出並加以研究的。

設G是R^N中的可測集，m(G)≠0，若f(x,u)滿足卡拉西奧多里條件，則運算元fφ=f(x,φ(x))稱為涅梅茨基運算元。

性質

涅梅茨基運算元將可測函式映為可測函式。

涅梅茨基運算元的一個重要性質是：如果fφ=f(x,φ(x))映入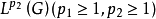，則f是連續運算元，並且是有界運算元。

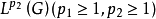
而f映入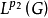的充分必要條件是存在常數b>0及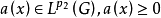，使得

對任給x∈G，u∈R¹成立。

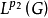
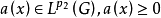
非線性運算元

非線性運算元又稱非線性映射，是不滿足線性條件的運算元。

泛函分析的研究對象主要是線性運算元及其特殊情況線性泛函。但是，自然界和工程技術中出現的大量問題都是非線性的。數學物理中的一些線性方程其實都是在一定條件下的近似。為研究這些非線性問題，涉及到的運算元（映射）將不能只局限於線性運算元。