基本介紹 謂詞演算除了一元
謂詞 ,也可以有二元 ,三元 ,甚至多元
謂詞 。事實上,數學中的關係,
函式 都可以看成
謂詞 。例如x≤y可以看成二元謂詞,x+y=z可以看成三元謂詞,因此謂詞演算的公式可表示數學中的一些命題。
謂詞可以在一定的個體
集合 中給出解釋,
謂詞公式 可以在這樣的個體集合中取到真假值。例如(*)在
實數集 R中解釋Q(x)為x是
有理數 ,則
謂詞公式 (*)取值為真。如果在R中解釋Q(x)為“x是整數”,
謂詞公式 (*)就取值為假了。
謂詞公式 在個體集合中取值的嚴格定義稱為基本語義定義,這個定義是波蘭籍數學家A.塔爾斯基在20 世紀 30年代給出的。給定了謂詞解釋的個體集合稱為模型。基本語義定義使謂詞公式和模型都可以被當作數學對象加以研究。一個謂詞公式在任意一個模型中都取真值,就稱之謂恆真式。兩個
謂詞公式 A,B在任意模型的任何一種解釋下都取相同的值,就稱A,B邏輯
等價 。
命題演算 中的恆真式和等價式所反映的規律在
謂詞演算 中仍成立。利用有關量詞的等價式作等價變換,可以把任何一個謂詞公式的量詞移到公式的最前面,得到與之等價的
前束 標準形公式。
推演規則 謂詞演算也可以
公理 化。從符號到公式的定義,從公理到推演都嚴格形式化,構成完全的公理系統,使系統所推演出的都是恆真式,且每個恆真式都能從公理推演出來。與
命題演算 不同的是,謂詞演算是一個不可判定的系統,即不存在一個算法來判定
謂詞公式 是否恆真式。
謂詞演算是命題演算的擴展,命題演算對於描述更複雜的數學結構是不充分的。從文法上說謂詞演算在現存的命題演算上增加了“謂詞-主詞結構”和量詞。主詞是給定的個體群組(集合)的一個成員的名字,而謂詞是在這個群組上的關係,一元謂詞在哲學中稱為性質,在數學中稱為
指示函式 ,在
數理邏輯 中稱為布爾值函式。
公理 謂詞演算的公理系統可引申到邏輯公理,命題演算公理等其它相關公理,按照這個順序,我們來介紹如下的公理系統。
構成 (1)符號庫(初始符號)
(2)形成規則(符號的使用)
(3)
公理 (推演的起點)
(4)變形規則(推演規則)
邏輯公理 下面描述謂詞演算中的
一階邏輯 公理。一個給定的一階理論有進一步的非邏輯公理。
對於任何理論,知道
公理 的集合是否可用算法生成,或是否存在算法確定合式公式為公理,是很有價值的。
如果存在算法在有限步驟後確定一個公式是否是公理,則公理的集合被稱為遞歸的或“可判定的”。在這種情況下,你還可以構造一個算法來生成所有的公理: 這個算法簡單的(隨著長度增長)一個接一個的生成所有可能的公式,而算法對每個公式確定它是否是個公理。
一階邏輯 的公理總是可判定的。但是在一階理論中非邏輯公式就不必需如此。
命題演算公理 命題演算公理 右圖的14條
公理 分成五組,在每一組符號中均出現蘊含號,而且還都是蘊含式,即公式形成時最後一次為蘊含運算。五組公理第一組中不再有其他符號,其餘四組依次出現一個新符號,它們是
合取 &
析取 V
否定 --和
等價 號(即
~ )。
注意,這14條公理顯然都是第一章
命題邏輯 中的永真公式,如果讀者懷疑其永真性,不妨用真值表方法去驗證一下。但是我希望讀者能直接看出每一條都是一個永真命題,即所謂的“重言式”。
等式公理 在
一階邏輯 中對使用等式(或
恆等式 )有多種不同的約定。本節總結其中主要的。不同的約定對同樣的工作給出本質上相同的結果,區別主要在術語上。
x = x
x = y → f(...,x,...) = f(...,y,...) 對於任何函式 f
x = y → (P(...,x,...) → P(...,y,...)) 對於任何關係 P (包括 = 自身)
其次常見的約定是把等號包含為理論的關係,並向這個理論的
公理 增加等式的公理。在實際中這是同前面約定最難分辨的,除了在沒有等式概念的不常見情況下。公理是一樣的,唯一的區別是把它叫做邏輯公理還是這個理論的公理。
在沒有
函式 和有有限數目個關係的理論中,有可能以關係的方式定義
等式 ,通過定義兩個項 s 和 t 是相等的,如果任何關係通過把 s 改變為 t 在任何討論下都沒有改變。例如,在帶有一個關係 ∈的
集合論 中,我們可以定義 s = t 為x (s ∈ x t ∈ x) ∧x (x ∈ s x ∈ t) 的縮寫。這個等式定義接著自動的滿足了關於等式的公理。
在某些理論中有可能給出特別的等式定義。例如,在帶有一個關係 ≤ 的
偏序 的理論中,我們可以定義 s = t 為 s ≤ t ∧ t ≤ s 的縮寫。
元邏輯定理 元邏輯定理 ①可靠性定理,即凡定理都是普遍有效的。 ②一致性定理。
一階邏輯 是一致的。若取只有一個個體a的集為
論域 ,αA(α)即為A(a),而所有
量詞 全部消去。於是,所有的公式都可看作是命題演算的公式。因此,對任一公式A,不可能A和非A都可證。
③完全性定理。
一階邏輯 在語義意義下是完全的,即凡普遍有效的公式都是定理。完全性定理還有一個更強的形式,即每一一致的公式集都有模型,都是可滿足的。這一更強形式的完全性定理也稱強完全性。
④緊緻性定理。一個公式集г是有模型的,若且唯若它的每一有窮子集是有模型的。根據一個比較容易證明的定理,公式集г是一致的,若且唯若它的每一有窮子集是一致的。緊緻性定理能直接從完全性定理推出。
可判定定理 謂詞演算最主要是在一階謂詞上的運算,下面列出了相關的一些重要的關於是否可判定的元邏輯定理。
有效性的判定問題是半可判定的。按
哥德爾完備性定理 所展示的,對於任何有效的公式 P,P 是可證明的。
一元
謂詞邏輯 (就是說,謂詞只有一個參數的謂詞邏輯)是可判定的。

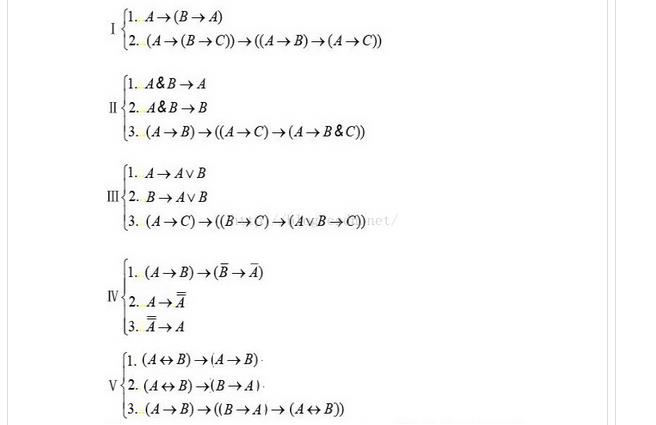 命題演算公理
命題演算公理
