基本介紹
- 中文名:切線長定理
- 外文名:Theorem of length of tangent
- 對象:圓
- 定義:從圓外一點可以引圓的兩條切線
- 所屬:幾何
- 套用學科:數學
- 推論:圓外切四邊形兩組對邊的和相等
內容
證明
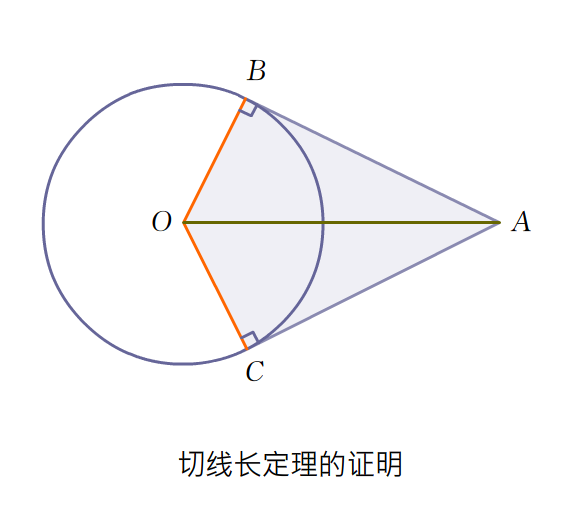 定理證明示意圖
定理證明示意圖
推論
推導過程
 例題
例題推廣(鑽石形)

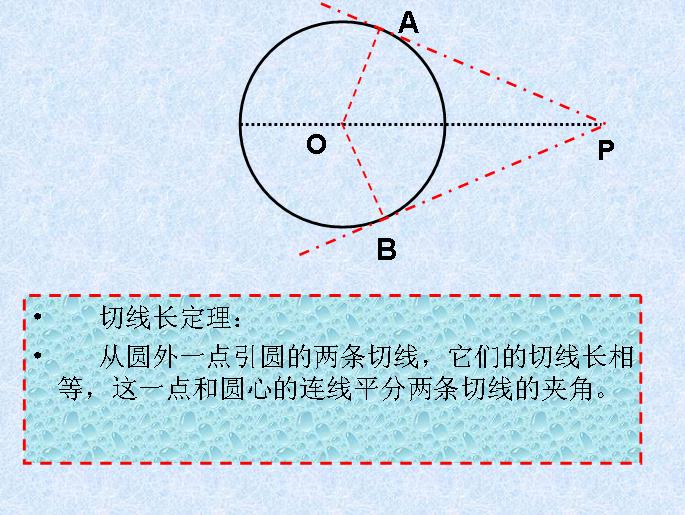
 定理證明示意圖
定理證明示意圖
 例題
例題
切線長定理(Theorem of length of tangent),是初等平面幾何的一個定理。它指出,從圓外一點引圓的兩條切線,它們的切線長相等。即如圖,AB、AC切圓O於B、C,...
切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項。切割線定理的推論:從圓外一點引圓的兩條割線,這一點到每條...
數學上的專用術語,指路線交點至曲線起點或終點的直線距離。常常用於圓的切線長及切線長公式。...
切線定理的內涵是:一直線若與一圓有交點,且只有一個交點,那么這條直線就是圓的切線。幾何上,切線指的是一條剛好觸碰到曲線上某一點的直線。
弦切線定理(英文名:Tangent chord theorem),是經過半徑的外端並且垂直於這條半徑的直線是圓的切線。...
圓的切線垂直於過其切點的半徑;經過半徑的非圓心一端,並且垂直於這條半徑的直線,就是這個圓的一條切線。 [2] 切線判定定理 一直線若與一圓有交點,且連線交點...
【例1】如圖,在⊙O中,⊙O的切線AC、BC交於點C.求證:∠CAB=∠CBA。解:∵AC、BC是⊙O的兩條切線∴AC=BC(切線長定理)∴∠CAB=∠CBA(等腰三角形中等邊...
斯特瓦爾特(Stewart)定理:設已知△ABC及其底邊上B、C兩點間的一點D,則有AB...③其在等腰三角形中的推廣,可用於求解與圓有關的問題(與圓的冪,切線長定理等...
切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項。 割線定理:從圓外一點P引兩條割線與圓分別交於A、B;C、D,...
布利安桑定理敘述如下:如果六邊形的邊交替地通過兩個定點P和Q,則連線六邊形的...由切線長定理易推出GB=BL,HE=KE,所以BE為圓O1和圓O3的根軸,...
切割線定理從圓外一點引圓的切線和割線,切線長是這點到割線與圓焦點的兩條線段長的比例中項 幾何語言:∵PT切⊙O於點T,PBA是⊙O的割線 ∴PT2=PA·PB(切割...
相交弦定理(Intersecting Chords Theorem),數學術語,是指圓內的兩條相交弦,被交點分成的兩條線段長的積相等或經過圓內一點引兩條弦,各弦被這點所分成的兩線段...
具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。...泰博定理馮奧貝爾定理密克爾點圓:垂徑定理圓周角定理弦切角定理切線長定理...
阿標定理可用初等幾何方法證得。證明定理可做輔助圓、運用切線長定理、焦點的性質,也可用代數方法。阿標定理意義 編輯 阿標定理填補了圓與拋物線中線段乘積與比例...
126切線長定理 從圓外一點引圓的兩條切線,它們的切線長相等, 圓心和這一點的連線平分兩條切線的夾角127圓的外切四邊形的兩組對邊的和相等...
(C.J.Brianchon)於1806年發現的,它的逆定理也成立,即:若簡單六線形的三對對頂點的連線共點,則此六線形外切於一個二級曲線,若給定二級曲線的六條切線,則可...
