弦切線定理

弦切線定理（英文名：Tangent chord theorem），是經過半徑的外端並且垂直於這條半徑的直線是圓的切線。

基本介紹

• 中文名：弦切線定理
• 外文名：Tangent chord theorem
• 套用學科：數學
• 適用領域範圍：幾何

英文名稱

弦切線定理

Tangent chord theorem

切線的判定和性質

切線的判定定理

經過半徑的外端並且垂直於這條半徑的直線是圓的切線 　幾何語言： ∵l ⊥OA，點A在⊙O上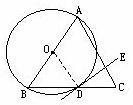

∴直線l是⊙O的切線（切線判定定理）

切線的性質定理

圓的切線垂直於經過切點半徑

幾何語言： ∵OA是⊙O的半徑，直線l切⊙O於點A

∴l ⊥OA（切線性質定理）

推論1 經過圓心且垂直於切線的直徑必經過切點

推論2 經過切點且垂直於切線的直線必經過圓心

切線長定理

從圓外一點引圓的兩條切線，它們的切線長相等，圓心和這一點的連線平分兩條切線的夾角

幾何語言： ∵直線PA、PB分別切⊙O於A、B兩點

∴PA=PB，∠APO=∠BPO（切線長定理）

切線長定理的基本圖像

證明：連結OA、OB

∵直線PA、PB分別切⊙O於A、B兩點

∴OA⊥AP、OB⊥PB

∴∠OAP=∠OBP=90°

在△OPA和△OPB中：

∠OAP=∠OBP

OP=OP

OA=OB=r

∴△OPA≌△OPB（HL）

∴PA=PB，∠APO=∠BPO

弦切角定理

弦切角（即圖中∠ACD)等於它所夾的弧(弧AC)對的圓周角等於所夾的弧的度數的一半等於1/2所夾的弧的圓心角 [注，由於網上找得的圖不是很完整，圖中沒有連結OC]

幾何語言：∵∠ACD所夾的是弧AC 　∴∠ACD=∠ABC=1/2∠COA=1/2弧AC的度數(弦切角定理）

推論 如果兩個弦切角所夾的弧相等，那么這兩個弦切角也相等

幾何語言：∵∠1所夾的是弧MN ，∠2所夾的是PQ ，弧MN = 弧PQ

弦切角的基本圖形

∴∠1=∠2

證明：作AD⊥EC

∵∠ADC=90°

∴∠ACD+∠CAD=90°

∵ED與⊙O切於點C

∴OC⊥ED

∴∠OCD=∠OCA+∠ACD=90°

∴∠OCA=∠CAD

∵OC=OA=r

∴∠OCA=∠OAC

∴∠COA=180°-∠OCA-∠OAC=180°-2∠CAD

又∵∠ACD=90°-∠CAD

∴∠ACD=1/2∠COA

∴∠ACD=∠ABC=1/2∠COA=1/2弧AC的度數

切割線定理

從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項。

　推論：從圓外一點引圓的兩條割線，這一點到每條割線與圓的交點的兩條線段長的積相等。

弦切角概念

頂點在圓上，一邊和圓相交、另一邊和圓相切的角叫做弦切角．它是繼圓心角、圓周角之後第三種與圓有關的角．這種角必須滿足三個條件：

（1）頂點在圓上，即角的頂點是圓的一條切線的切點；

（2）角的一邊和圓相交，即角的一邊是過切點的一條弦所在的射線；

（3）角的另一邊和圓相切，即角的另一邊是切線上以切點為端點的一條射線．

它們是判斷一個角是否為弦切角的標準，三者缺一不可，比如下圖中 均不是弦切角．

（4）弦切角可以認為是圓周角的一個特例，即圓周角的一邊繞頂點旋轉到與圓相切時所成的角．正因為如此，弦切角具有與圓周角類似的性質．