頂點在圓上,一邊和圓相交,另一邊和圓相切的角叫做弦切角。其大小等於它所夾的弧所對的圓周角。
基本介紹
- 中文名:弦切角
- 外文名:angle of osculation
- 大小等於:它所夾的弧所對的圓周角
- 特點:頂點在圓上
定義

特徵識別
弦切角定理
 圖2
圖2套用

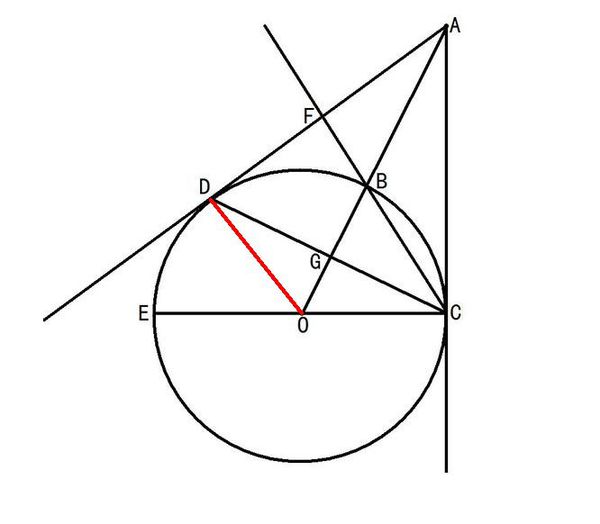
頂點在圓上,一邊和圓相交,另一邊和圓相切的角叫做弦切角。其大小等於它所夾的弧所對的圓周角。

 圖2
圖2
頂點在圓上,一邊和圓相交,另一邊和圓相切的角叫做弦切角。其大小等於它所夾的弧所對的圓周角。...
弦切角定理:弦切角的度數等於它所夾的弧所對的圓心角度數的一半,等於它所夾的弧所對的圓周角度數。與圓相切的直線,同圓內與圓相交的弦相交所形成的夾角叫做弦切角...
幾何語言:∵∠ACD所夾的是弧AC ∴∠ACD=∠ABC=1/2∠COA=1/2弧AC的度數(弦切角定理)推論 如果兩個弦切角所夾的弧相等,那么這兩個弦切角也相等...
所屬學科 數學(幾何學) 相關概念 切線,割線,弦切角定理等 目錄 1 基本介紹 2 切割線定理的證明 3 例題解析 切割線定理基本介紹 編輯 切割線定理:從圓外一...
,也就是偏角,也叫弦切角。點P 處,切線與弦線的夾角為從原點開始沿迴旋線行走距離 ,到達緩圓點HY,即迴旋線的長度為圓曲線的半徑為R在...
弦切角定理:弦切角等於它所夾的孤對的圓周角.它是圓中證明角相等的重要定理之一.切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條...
弦切角定理弦切角等於它所夾的弧對的圓周角 幾何語言:∵∠BCN所夾的是 ,∠A所對的是 ∴∠BCN=∠A 推論如果兩個弦切角所夾的弧相等,那么這兩個弦切角也相等 ...
弦切角定理:弦切角等於它所夾的弧對的圓周角,它是圓中證明角相等的重要定理之一。 [4] 切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點...
(5)弦切角的度數等於它所夾的弧的度數的一半。(6)圓內角的度數等於這個角所對的弧的度數之和的一半。(7)圓外角的度數等於這個角所截兩段弧的度數之差的一半...
首先,由弦切角定理可以得到:sin∠ACR=sin∠ABCsin∠BCR=sin∠BACsin∠BAP=sin∠BCAsin∠CAP=sin∠ABCsin∠CBQ=sin∠BACsin∠ABQ=sin∠BCA...
圖Ⅲ:切割線定理。如圖,連線AC、AD。∠PAC為切線PA與弦AC組成的弦切角,因此有∠PBC=∠D,又因為∠P為公共角,所以有 ,易證圖Ⅳ:切線長定理。PA、PC均為切線...
