基本介紹
- 中文名:分配格
- 外文名:distributive lattice
- 所屬學科:數學(格論)
- 簡介:一種組合構形
- 舉例:布爾格、除數格、理想格、鏈等
基本介紹
 分配格
分配格舉例分析
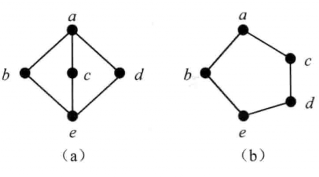 圖1
圖1 分配格
分配格 圖1
圖1分配格是一種組合構形,它是滿足下述條件的格:對於格的任意元素x,y和z,均有x∧(y∨z)=(x∧y)∨(x∧z)。由於格中結運算和交運算的對稱性,上述條件等價...
分配格模(distributive lattice-ordered module)一類重要的格模.設Mx是格模,若對任意.},yEM,rER+,有:則稱Mx為分配格模.即對於rER+的乘法是M的格同態.對於格...
分配格序環(distributive lattice ordered ring )亦稱d環,一類滿足乘法對交、並的分配律的格環.設R是格環,若對任意二,yER,lxyl=}二}}川,則稱R為分配格序...
分配格序半群(distributive lattice-ordered se-migroup)一類重要的格序半群.設S是格序半群,若作為格,<S,八,V)是分配的,則S稱為分配格半群. ...
有補格(complemented lattice)亦稱有餘格,是一種特殊的有界格,在有界格〈L,≤〉中,對於L中的任意元素a,如果存在b∈L,使得a+b=1,a·b=0,則稱元素b是...
模格(modular lattice)亦稱戴德金格,是格論中僅次於分配格的一類重要格,設L是格,對任意a,b,c∈L,若L滿足下列條件之一:L5:若a≤c,則a∨(b∧c)=(a∨b)...
格序群(lattice-ordered group)亦稱格群或l群,是一種具有格序關係的群。若偏序群G作為偏序集是格,則稱G為格序群。格群是分配格。數學中,“格”一種特殊的...
在數學中,布爾格是與布爾代數有密切關係的一類格,一個有補分配格稱為布爾格,由一個布爾格〈L,≤〉可以誘導出一個布爾代數〈L,·,+,′,0,1〉,在布爾格〈...
通過考慮不同的帶有適當的理想概念的數學結構可獲得其他定理,例如環和(環論的)素理想,和分配格和(序理論的)的極大理想。本文關注序理論的素理想定理。...
《一般格論基礎》作者:李海洋出版時間:2012-11...... 與格,主要包括格的類型,格的理想、濾子、同餘,Galois聯絡等;第3章論述了分配格的基本內容,著重討論了分配...
*有界格,設(L,£)是格,如果L有最大元素(記作1)和最小元素(記為0),則(L,£)稱為有界格,記作(L,£,1,0)或(L,*, °,0,1)...
菱形格(diamond-type lattice ) 一類特殊的子格.典型的非分配格,但它是模格.格1.的子集A稱為菱形格若且唯若A是與M}同構的子格,其中M。...
《現代數學基礎43:格論導引》講述格論的基本概念與基礎知識。其內容涵蓋:有序集、保序映射、格與半格、完全格、理想與同態、格同餘等基本概念;模格與半模格;...
