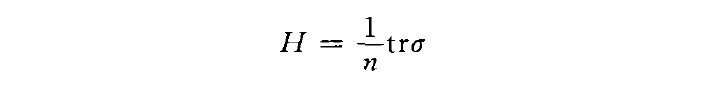
具平行平均曲率的子流形(submanifolds withparallel mean curvature)一類重要的子流形.指平均曲率向量在法叢中平行的子流形。
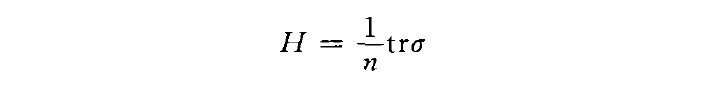
具平行平均曲率的子流形(submanifolds withparallel mean curvature)一類重要的子流形.指平均曲率向量在法叢中平行的子流形。設M"為黎曼流形N‘的n維子流形，。為M"的第二基本形式，為...
（1）子流形的Bernstein問題方面。我們一是研究了一類Calibrated流形中具有平行平均曲率向量和Calibrated角餘弦具有某種增長條件的子流形，給出了這類流形中具有任意維數和余維數子流形的Bernstein型結果。二是研究了一類非平坦偽黎曼流形中滿足某種條件的極大類空子流形，並在一定條件下證明了該子流形必是一線性映射...
獲得了截面曲率拼擠條件下常曲率空間形式中4維緊緻Einstein子流形的最佳剛性定理； 證明了正數量曲率緊緻Einstein流形的剛性定理。將廣義Ejiri剛性定理推廣到局部對稱空間中平行平均曲率子流形的情形，證明了Ricci曲率拼擠條件下正pinched黎曼流形中平行平均曲率子流形的分類定理。本課題具有重要的理論意義和套用價值。
證明了積分型拼擠條件下歐氏空間中具有平行Gauss平均曲率的子流形的空隙定理。證明了拼擠流形中緊緻平行平均曲率子流形的幾何剛性定理。在關於數量曲率和截面曲率的拼擠條件下，證明了黎曼流形的分類定理和微分球面定理。在最佳化截面曲率拼擠條件下，證明了空間形式中緊緻子流形的微分球面定里。獲得了歐氏空間中緊緻超...
實質性地改進了球面中緊緻極小子流形的Ejiri剛性定理和丘成桐剛性定理。證明了空間形式中緊緻平行平均曲率子流形的廣義Ejiri剛性定理和廣義丘成桐剛性定理。獲得了球面中緊緻平行平均曲率子流形的一個最佳外蘊剛性定理。證明了曲率積分拼擠條件下空間形式中任意余維平均曲率流解的收斂性定理和可延拓性定理。獲得了雙曲...
本項目的研究目標是半黎曼流形（包括黎曼流形）中子流形的幾何性質，重點是其中的極小或極大子流形，同時對別的類型的子流形如平行平均曲率子流形、旋轉型子流形、等參超曲面等也予以關注。因為研究期限為四年，本項目將對當代微分幾何中幾個重要的未解決問題開展研究，期望能獲得突破。結題摘要 半黎曼流形也叫...
由於理論物理的需要，對半黎曼流形中子流形幾何性質的研究，同時受到微分幾何學家和理論物理學家的關注。常曲率的半黎曼流形稱為半黎曼空間型。本項目通過運用變分方法，對子流形作形變，來研究半黎曼空間型中子流形的幾何性質，重點是研究其中的極小或極大子流形。同時對別的類型的子流形如平行平均曲率子流形、...
獲得了球面中任意余維平均曲率流在曲率積分拼擠條件下的光滑收斂定理及其拓撲套用。得到了空間形式中保體積平均曲率流的光滑收斂定理。證明了平均曲率流的光滑延拓定理。證明了一類黎曼流形上Ricci流的曲率估計與光滑收斂定理。得到了一類共形平坦黎曼流形上Yamabe流的光滑收斂定理。證明了球面中平行平均曲率子流形關於不變數...
正則子流形是特殊的子流形，設微分流形N的子流形為M，如果是一個同胚，那么稱M是N的正則子流形，並稱為M在N中的正則嵌入。簡介 n維流形M的一個正則子流形S，是M的一個子集，使得對任何點 ，流形M的極大圖冊中存在坐標卡 ，其中 並且 。其中，s是一個整數，稱為S的維數。閉子流形 設M是一個流形，M...
是微分幾何中的子流形幾何。 包括滿足特殊的幾何或拓撲條件的子流形的結構性問題, 關於空間形式中極小子流形以及具有平行平均曲率的子流形, 常量曲率子流形, 雙調和子流形等的最佳幾何剛性、幾何分類問題， 以及黎曼流形中子流形的變分問題, 空間形式中特殊子流形的構造等研究.教學特色：教學認真負責，內容明確，...
主要工作包括利用全純曲線理論對球面中極小浸入曲面的研究、六維球面中具有常數Kaehler角的一類極小浸入曲面的分類定理、歐氏空間中高余維浸入曲面的G*-形變、空間形式中具有平行平均曲率向量場和常數量曲率的子流形的Moebius刻畫、球面中具有平行Blaschke張量的超曲面、具有平行仿Blaschke張量的超曲面的完全分類、以及有關...
通過引進新的內蘊不變數，將關於正曲率黎曼曲面的阿達瑪微分球面定理完整推廣到n維黎曼流形的情形。證明了具有正數量曲率的黎曼流形的微分球面定理。部分解決了關於黎曼流形逐點Pinching問題的丘成桐猜想。（3）證明了球面中平行平均曲率子流形的廣義陳省身-do Carmo-Kobayashi定理，並給出了數量曲率達到臨界值時流形的...
18.《具有平行平均曲率的三維子流形的2-調和等距浸入》哈爾濱師範大學自然科學學報 1995，11 19.《Euler 示性式在子流形上的積分公式》哈爾濱師範大學自然科學學報 1990，10 20.《Ω（M:N₁,N₂）中臨界點存在性的證明》哈爾濱師範大學自然科學學報 1996，2 21.《基本群胚上的動量映射》哈爾濱師範大學自然科學...
