在代數中,一個多項式是一個六項式的多項式。六次方程式或六元方程式是六度多項式方程式,即左手側是一個多項式並且右側為零的方程式。
基本介紹
- 中文名:六次方程
- 外文名:Sextic equation
- 定義:左側是多項式並且右側為零的方程
- 套用學科:數學
- 相關術語:六次函式
- 套用:蒸汽機早期設計中出現的瓦特曲線
定義


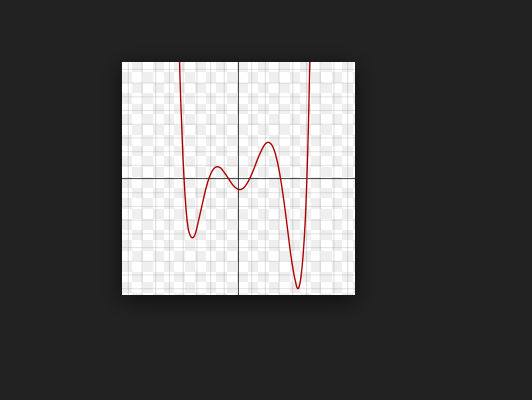
在代數中,一個多項式是一個六項式的多項式。六次方程式或六元方程式是六度多項式方程式,即左手側是一個多項式並且右側為零的方程式。


在代數中,一個多項式是一個六項式的多項式。六次方程式或六元方程式是六度多項式方程式,即左手側是一個多項式並且右側為零的方程式。定義六次方程是可以用下式表示的方程其中a≠ 0。 而六次函式是可以用下式表示的函式:其中a≠ ...
一元六次方程是指在一個等式中,只含有一個未知數,且未知數的最高次數是6次的整式方程。方程標準 形如aX^6+bX^5+cX^4+dX^3+eX^2+fX+g=0的方程是一元六次方程的標準型 發展歷史 16 世紀時,義大利數學家塔塔利亞和卡當等人...
六次函式是數學科的一條定律。一般的,自變數x和因變數y存在如下關係y=ax^6+bx^5+cx^4+dx^3+ex^2+fx+g的函式,稱y為x的六次函式。基本定義 方程中a、b、c、d、e、f分別為六次、五次、四次、三次、二次、一次項係數...
方程(equation)是指含有未知數的等式。是表示兩個數學式(如兩個數、函式、量、運算)之間相等關係的一種等式,使等式成立的未知數的值稱為“解”或“根”。求方程的解的過程稱為“解方程”。通過方程求解可以免去逆向思考的不易,...
使得方程中等號兩邊相等的未知數的值叫做方程的解;也可以說是方程中未知數的值叫做方程的解。只含有一個未知數的方程的解叫方程的根。x=2 是方程2x-4=0的解,也是該方程的根。方程解法 一元三次方程的求根公式用通常的演繹思維是...
不一定放在方程左邊,或一個方程式子裡有兩個 ,這樣就要用數學中的簡便計算方法去解決它了。有些式子右邊有 ,為了簡便算,可以調換位置。方程分類 一元二次方程 就是關於平方的方程 解一元二次方程的基本思想方法是通過“降次”將它...
常微分方程,屬數學概念。學過中學數學的人對於方程是比較熟悉的;在初等數學中就有各種各樣的方程,比如線性方程、二次方程、高次方程、指數方程、對數方程、三角方程和方程組等等。這些方程都是要把研究的問題中的已知數和未知數之間的...
華羅庚在論文的開頭寫道:五次方程經 Abel,Galois 之證明後,一般算學者均認為不可以代數解矣,而《學藝》7卷 10 號載有蘇君之《代數的五次方程式之解法》一文,羅欣讀之而研究之,於去年冬也仿得‘代數的六次方程式之解法’矣,羅...
都算是二次項,而 算0次項,方程 中每一項都是0次項,所以是“齊次方程”。2、形如y''+py'+qy=0的方程稱為“齊次線性方程”,這裡“齊次”是指方程中每一項關於未知函式y及其導數y',y'',……的次數都是相等的(都是...
十一世紀,阿拉伯的阿爾·卡爾希第一次解出了二次方程的根。十一世紀,阿拉伯的卡牙姆完成了一部系統研究三次方程的書《代數學》。十一世紀,埃及的阿爾·海賽姆解決了“海賽姆”問題,即要在圓的平面上兩點作兩條線相交於圓周上一點,並...
整式方程未知數次數最高項次數高於2次的方程,稱為高次方程。高次方程解法思想是通過適當的方法,把高次方程化為次數較低的方程求解。對於5次及以上的一元高次方程沒有通用的代數解法和求根公式(即通過各項係數經過有限次四則運算和...
只含有一個未知數(即“元”),並且未知數的最高次數為5(即“次”)的整式方程叫做一元五次方程(英文名:Quintic Equation with one unknown)。一元五次方程的標準形式(即所有一元五次方程經整理都能得到的形式)是ax⁵+bx...
六字及以上 一元一次方程 一元二次方程 完全平方公式 最簡二次根式 直接開平方法 半開半閉區間 萬能置換公式 絕對值不等式 實係數多項式 復係數多項式 整係數多項式 不等邊三角形 中心對稱圖形 基本初等函式 基本積分公式 ...
這個定理簡單地說就是n次方程有n個根。1742年12月15日瑞士數學家歐拉曾在一封信中明確地做了陳述,後來另一個數學家、德國的高斯在1799年給出了嚴格的證明。把上面分析過的內容綜合起來,組成初等代數的基本內容就是:三種數——有理...
四次方程笛卡爾法 一般的四次方程還可以待定係數法解,這種方法稱為笛卡爾法,由笛卡爾於1637年提出。先將四次方程化為x⁴+ax³+bx²+cx+d=0的形式。令x=y-a/4 整理後得到y⁴+py²+qy+r=0 (1)設y⁴+py²+...
初等代數學進一步地向兩個方面發展,一方面是研究未知數更多的一次方程組;另一方面是研究未知數次數更高的(一元)高次方程。這時候,代數學已由初等代數向著高等代數的方向發展了,相應地也形成了”線性代數“與”(一元)多項式代數“兩...
數學中用以求解高次一元方程的一種方法。把方程的一側的數(包括未知數),通過移動使其值化成0,把方程的另一側各項化成若干因式的乘積,然後分別令各因式等於0而求出其解的方法叫因式分解法。因式分解 (factorization of polynomials)...
堅定地對他的老師說:“讓我來解答這一歷史難題吧,我能證明四次以上的方程是否有解。”他憑著自信,聰明和勤奮,花了六年的時間,給了歷史一個圓滿的回答:一般高於四次的方程沒有代數解。這就是著名的阿貝爾-魯菲尼定理。
在長篇論文《關於方程的代數解法的思考》(Réflexions sur le resolution algébrique desequations,《全集》Ⅲ, pp 205—421)中,把前人解三、四次代數方程的各種解法,總結為一套標準方法,而且還分析出一般三、四次方程能用代數...
那么到了複數範圍內是不是仍然有代數方程沒有解,還必須把複數再進行擴展呢?數學家們說:不用了。這就是代數裡的一個著名的定理——代數基本定理。這個定理簡單地說就是n次方程有n個根。1742年12月15日瑞士數學家歐拉曾在一封信中...
該書中解決了某些一次、二次方程問題和不定方程問題,出現了縮寫符號和套用負數之例。其問題構思精巧,解題方法極多,但最大的缺點是沒有解方程的一般方法。發展 算術 代數之前已有算術,算術是解決日常生活中的各種計算問題,即整數與...
求一元3次方程3個解的程式:Py代碼 Python代碼以實例展示求解方程 的根。Java代碼 Java實現開平方的牛頓疊代法. 求 的算術平方根就是求 的正根, 得疊代公式: . 代碼中取初始值 , 誤差控制在 .Fo代碼 program newton 其他...
定義4:在平面直角坐標系中,二元二次方程F(x,y)=Ax²+2Bxy+Cy²+2Dx+2Ey+F=0滿足以下條件時,其圖像為雙曲線。1、係數矩陣滿秩,即 2、Δ=B²-AC>0 在高中的解析幾何中,學到的是雙曲線的中心在原點,圖像關於x,...
《高等代數(第五版)》主要內容是:多項式、行列式、線性方程組、矩陣、二次型、線性空間、線性變換、λ-矩陣、歐幾里得空間、雙線性函式與辛空間、總習題,附錄包括關於連加號“∑”、整數的可除性理論、代數基本定理的證明、A-矩陣...
