基本介紹
- 中文名:一元六次方程
- 係數:a b c d e f
- 常數:g
- 條件:a,b,c,d,e,f,g∈R,且a≠0
- 阿貝爾定理:不存在一般五次方程求根公式
- 可否解:普遍不可
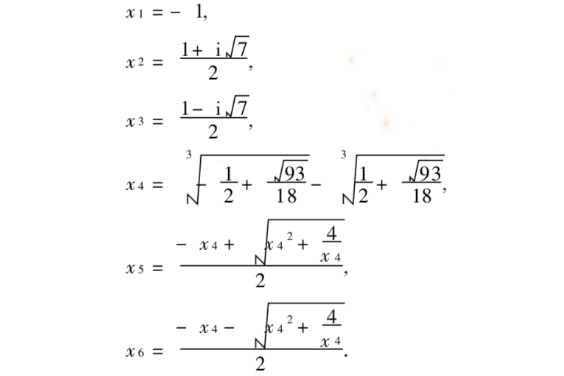
一元六次方程是指在一個等式中,只含有一個未知數,且未知數的最高次數是6次的整式方程。方程標準形如aX^6+bX^5+cX^4+dX^3+eX^2+fX+g=0的方程是一元六次方程的標準型發展歷史16 世紀時,義大利數學家...
§6.1 一元五次方程解 §6.2 一元六次方程解 §6.3 代數基本定理 §6.4 無窮階代數方程解探索 第七章 複數 §7.1 虛數的引入 §7.2 複數的意義與表示 §7.3 複數的數學套用 §7.3a 複數與平面幾何 §7.3b 複變函數...
解出參數a。這樣原方程兩邊都是完全平方式,開方後就是一個關於x 的一元二次方程,於是就可以解出原方程的根x。最後,對於5次及以上的一元高次方程沒有通用的代數解法(即通過各項係數經過有限次四則運算和乘方和開方運算),這稱為...
數學的基本概念之一,指使的一些計算規則,算術中有加、減、乘、除、乘方、開方六種運算,其中加、減、乘、除是從兩個已知數得出第三個數的運算,稱為二元運算;乘方、開方是從一個已知數得出另一個數的運算,稱為一元運算。
式 ⒁只是一元三方程的一個實根解,按韋達定理一元三次方程應該有三個根,不過按韋達定理一元三次方程只要求出了其中一個根,另兩個根就容易求出了。x^y就是x的y次方好複雜的說塔塔利亞發現的一元三次方程的解法一元三次方程的...
例如x+1=0可看成x,y的二元方程x+0y+1=0,它在平面直角坐標系中表示一條直線。基本介紹 在數域F上只含有一個未知數的方程,叫做F上的一元方程,一元一次方程、一元二次方程等都是一元方程。一元方程的解又叫做方程的根。含有...
“次”:方程中次的概念和整式的“次”的概念相似。指的是含有未知數的項中,未知數次數最高的項。而次數最高的項,就是方程的次數。“解”:方程的解,指使,方程的根是方程兩邊相等的未知數的值,指一元方程的解,兩者通常可以...
一元n次方程(equation of degree n with one unknown)是一元n次多項式所確定的方程,指方程a₀xⁿ+a₁x+…+aₙ=0 (a₀≠0),當n≥3時,稱為高次方程.研究一元n次方程的根,包括根的存在、根式解、根的界和根的個...
求一元五次方程的根式解曾困擾數學家三百餘年,阿貝爾和伽羅瓦的工作證明了一般一元五次方程沒有根式解。1930 年華羅庚《蘇家駒之代數的五次方程式解法不能 成立之理由》一文,是對試圖推翻阿貝爾和伽羅瓦證明的一種反駁,也是華羅庚的成名...
初等代數學進一步地向兩個方面發展,一方面是研究未知數更多的一次方程組;另一方面是研究未知數次數更高的(一元)高次方程。這時候,代數學已由初等代數向著高等代數的方向發展了,相應地也形成了”線性代數“與”(一元)多項式代數“兩...
初等代數學進一步地向兩個方面發展,一方面是研究未知數更多的一次方程組;另一方面是研究未知數次數更高的(一元)高次方程。這時候,代數學已由初等代數向著高等代數的方向發展了,相應地也形成了”線性代數“與”(一元)多項式代數“兩...
19世紀之前的300年間,數學家們一直為證明一元四次以上的方程是否有解而忙碌著,可惜他們不是望而卻步,就是半途而廢,沒有一位能揭開這個結。1818年,挪威一位16歲的男孩,在研究了前人的有關這一問題的大量資料後,堅定地對他的...
六 函式及其圖象 1平面直角坐標系 坐標平面 坐標平面內點的 坐標 坐標平面內的兩個基本公式 常量與變數 函式 函式的表示法 函式的自變數 取值範圍的確定 正比例函式 反比例函式 一次函式 二次函式 一元二次函 數與一元二次方程 一元...
二、根據恆等條件,列出一組含待定係數的方程。在這一題中,恆等條件是:2-A=1 B=0 C=-5 三、解方程或消去待定係數,從而使問題得到解決。∴A=1 B=0 C=-5 四次方程笛卡爾法 一般的四次方程還可以待定係數法解,這種方法稱...
1)因式分解與解高次方程有密切的關係。對於一元一次方程和一元二次方程,國中已有相對固定和容易的方法。在數學上可以證明,對於一元三次方程和一元四次方程,也有固定的公式可以求解。只是因為公式過於複雜,在非專業領域沒有介紹。對...
7.5實係數一元四次方程 7.6復係數一元二次方程(1)7.7復係數一元二次方程(2)7.8小結 第8章解一元n次方程(下)8.1實係數一元代數方程 8.1.1求解實係數一元五次方程的根 8.1.2求解實係數一元六次方程的根 8.1.3求解...
(3)不解方程,求根的對稱式的值(455―460)(4)求作以某兩數為根的二次方程(461―465)(5)幾個一元二次方程的公共根(466―470)(6)已知根具有某性質,求係數的值或取值範圍(471―485)4.高次方程 (1)一元三次...
最簡二次根式 同類二次根式 同次根式 異次根式 二次根式加減法法則 二次根式乘法法則 二次根式除法法則 分母有理化 有理化因式 分母有理化的兩種基本 類型 十一 一元二次方程 整式方程 一元二次方程 直接開平方法解一元二次 方程 ...
9.2 高次方程 9.2.1 一元n 次方程的根的個數 9.2.2 一元n 次方程的根與係數的關係 9.2.3 一元n 次方程的根的性質 本章習題 第10章 不等式的證明 10.1 比較法 10.2 分析法 10.3 綜合法 10.4 反證法 本章習題 ...
當D=0時,方程(1)有三個實根,當p,q均不為0時,有兩個重根和一個單根;當D 卡爾達諾公式表明三次方程有根式解,他的學生費拉里(L.Ferrari)用降階法獲得一元四次方程的根式解法,從而引發了人們對五次以上代數方程的根式解的...
