基本介紹
- 中文名:卡爾達諾公式
- 外文名:Cardano formula
- 所屬學科:數學(高等代數)
- 別名:卡爾丹公式
- 簡介:三次方程的求解公式
基本介紹



相關介紹







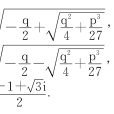










1545年,義大利學者卡丹(也翻譯為卡爾達諾)(Cardano G.,1501-1576年)所著的《關於代數的大法》中給出了一元三次方程x³+px+q=0,(p,q∈R)的求根公式,人們就將這個公式稱為卡丹公式或卡爾達諾公式。對標準型的一元三次方程...
代數:在1545年出版的《大術》一書中,他第一個發表了三次代數方程一般解法的卡爾達諾公式,也稱卡當公式(解法的思路來自塔塔利亞,兩人因此結怨,爭論經年)。書中還記載了四次代數方程的一般解法(由他的學生費拉里發現)。此外,...
公式簡介 解一元三次方程問題是世界數學史上較著名且較為複雜而又有趣味的問題,虛數概念的引進、複數理論的建立,就是起源於解三次方程問題。1545年,義大利學者卡爾丹(Cardano,1501—1576,又譯作卡爾達諾)發表了三次方程X^3+pX+q...
7. 口吃者的秘密:卡爾達諾公式 8. 九重天上的秩序:克卜勒的行星運行定律 9. 書寫永恆:費馬最後定理 10. 一片未曾探索過的大陸:微積分基本定理 11. 關於蘋果、傳說……以及彗星:牛頓定律 12. 偉大的探索者:歐拉定理 第三部分...
當卡丹試圖用該公式解方程x³-15x-4=0時,他的解是:x=[2+(-121)^(1/2)]^(1/3)+[2-(-121)^(1/2)]^(1/3)在那個年代負數本身就是令人懷疑的,負數的平方根就更加荒謬了。因此卡丹的公式給出x=(2+j)+(2-j)=...
三次方程的求根公式以“卡爾達諾公式”流傳下來。四次方程的一般解法由卡爾達諾的學生費拉里得到。在出現普遍適用的代數符號之前,代數方程理論的發展是緩慢的、曲折的。花拉子米的《代數學》完全用文字敘述,使用起來很不方便。丟番圖和...
四次方程的求根公式由卡爾達諾的學生費拉里首先得到,也記載於卡爾達諾的《大術》中。在16世紀末到17世紀上半葉,數學家們還探討如何判定方程的正根、負根和復根的個數。卡爾達諾曾指出一個實係數方程的復根是成對出現的,牛頓在他的《...
三次方程的求根公式也因此被稱為卡爾達諾公式或卡當公式。塔爾塔利亞與費拉里的論戰 卡爾達諾的行為激怒了正埋頭翻譯、注釋《幾何原本》的塔爾塔利亞。1546年塔爾塔利亞出版了一部題為《各種問題和發明》(Quesiti et inventioni diverse)的...
由於卡爾達諾最早發表了求解一元三次方程的方法,因而該解法至今仍被稱為“卡爾達諾公式”。在《大術》中同時發表的還有費拉里的一元四次方程一般解法。成就 除了一元三次方程的求解外,費羅還對分數的有理化做出了重要的貢獻,他將分母從...
這些小冊子不僅包括算術、幾何、代數問題,而且還有地理、天文、建築等內容,生動地反映了16世紀義大利的精密科學的狀況,其中有些內容又寫進了《數量概論》一書中.無論如何,三次方程的解法如今稱為“卡爾達諾”公式,這是誤稱.在該書...
7. 口吃者的秘密:卡爾達諾公式 8. 九重天上的秩序:克卜勒的行星運行定律 9. 書寫永恆:費馬最後定理 10. 一片未曾探索過的大陸:微積分基本定理 11. 關於蘋果、傳說……以及彗星:牛頓定律 12. 偉大的探索者:歐拉定理 第三部分...
25.阿達莫斯與六邊形幻方 26.勤學善算的數學家——楊輝 27.少年有為的帕斯卡 28.促成一位數學家的趣題 29.第一次數學危機——無理數的誕生 30.蜜蜂的啟示 31.代數學之父——韋達 32.結巴數學家與卡爾達諾公式 ……後記 ...
二次方程配方後只有左邊有x,可以兩邊開平方求解。三次方程配方後,方程的兩邊都有x,所以無法直接開立方求解,我們必須要尋找新方法解出x+2的值才行(這個所謂的新方法就是卡丹公式法)。 令y=x+2,於是得到了消去二次項的方程(即x=...
