基本介紹
- 中文名:兩人零和對策
- 外文名:two person zero-sum game
- 提出者:約翰·馮·諾伊曼
定義
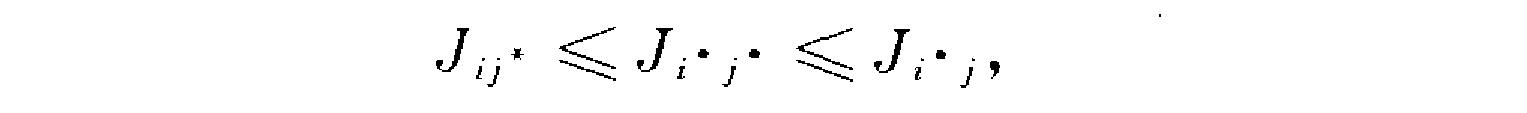

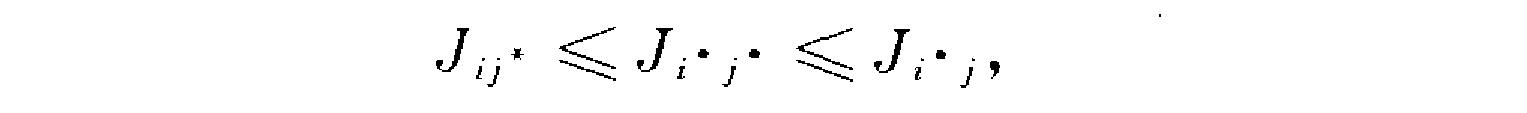
兩人零和對策(two person zero-sum game ) 模型,是一種最基本的完全對抗情形的對策模型.最初是由著名數學家約翰·馮·諾伊曼(John von Neuman)所提出,後來又由麻省理工學院的經濟學家萊...
所謂二人零和對策是指參與對策的局中人只有兩個每個人的策略集均為有限集且兩個局中人的贏利之和為零(或某個常數)。對策論中理論最簡單又最完善的部分是二人零和對策,它是其他各部分理論的基礎。許多遊戲都可看作是二人零和對策的...
二人有限零和對策是兩個局中人都有有限個可供選擇並能作出最優決策的策略。這種策略付諸實施的結果是產生平衡局勢,即參與對策的兩個局中人在更換掉原先選定的策略後所產生的新局勢的贏得都比原來的局勢要小,所以,一般來說,參與對策...
兩人無限零和對策(two-person infinite zero-sum game )是2016年公布的管理科學技術名詞,出自《管理科學技術名詞》第一版。定義 策略集中至少有一個是無限集合,支付之和總為零的一類對策。出處 《管理科學技術名詞》第一版。
動態兩人零和對策(dynamic two-person zero-sum game)一種微分對策.指微分對策問題中對抗雙方得失相抵,其和為零的對策.在定量微分對策中,參與對策的雙方具有相同形式的目標函式(性能指標),一方要選取其策略,使此函式取最小可能的值...
。具有上述條件的對策稱為嚴格決定對策,稱為這個對策的值。當這一關係不成立時,就稱為非嚴格決定對策。兩人零和對策與嚴格決定對策 人們在競爭或鬥爭中,總希望自己的一方取勝.每一方為取勝所作的努力一定會遭到對手的干擾,因此,任何...
對該準則下的最佳化問題,在離散時間兩人零和隨機對策的框架下,建立了Shapley方程,得到了值函式和鞍點存在的條件,給出了近似計算值函式的疊代算法、誤差估計和策略對是鞍點的兩個等價條件。相應結果發表在學術期刊Optimization上。 上述...
兩人對策 兩人對策(two-person game )是2016年公布的管理科學技術名詞,出自《管理科學技術名詞》第一版。定義 兩個局中人參與的對策。出處 《管理科學技術名詞》第一版。
零和對策模型 零和對策模型(zero sum game model)是1990年公布的自動化科學技術名詞。公布時間 1990年,經全國科學技術名詞審定委員會審定發布。出處 《自動化名詞》第一版。
.其次, V (S)應為下列兩人零和問題的解:以S的成員結盟為一方力圖使其總收益最大,而以S以外成員結盟為另一方併力圖使S的總收益為最小.此外,若S 和T為任意兩個不相交的對局人子集,則形成結盟的首要條件自然是 具這種性質的...
1928年美籍匈牙利數學家 J·von·諾伊曼在研究對策論時已發現線性規劃與對策論之間存在著密切的聯繫。兩人零和對策可表達成線性規劃的原始問題和對偶問題。他於1947年提出對偶理論。1951年G.B.丹齊克引用對偶理論求解線性規劃的運輸問題,...
對策論 為適應軍事鬥爭需要而出現較早的一種競爭性決策理論。當參加競爭的只限於敵我雙方,而競爭的結果是一方所得等於另一方所失,即“得失”相加等於零,這種對策稱為兩人零和對策。如果競爭是非對抗性的,即競爭雙方有可能在不同程度上...
這裡考慮的是一個動態兩人零和對策: 式中Xₖ={x(k)},Yₖ={y(k)}分別表示局中人Ⅰ和局中人Ⅱ在k時刻的策略集,Aₖ是依賴於策略x(k)和y(k)的局中人Ⅰ的贏得函式,z(k)是狀態變數,fₖ(·)是某個函式,當初態...
三、二人零和博奕:這一部分包括第3、4兩章,主要結論是“馮·諾依曼最小最大定理”,該定理是1928年馮·諾依曼在創立博奕論理論基礎時提出來的。四、具有合作對策的三人以上博奕: 這一部分包括從第5章到第12章的8章內容。討論了多...
靜態對策 包括: 結盟對策。其中包括聯合對策、合作對策。 不結盟對策。其中包括:有限對策、無限對策。 有限對策主要有:兩人有限零和對策、兩人有限非零和對策、三人有限零和對策、三人有限非零和對策。無限對策。主要有:兩人無限零和對策、...
(4) 零和對策。在任一“局勢”中,決策者的“贏得”等於競爭對手的“損失”或者相反。對抗型決策可按以下標誌分類:按競爭對手多少分為兩人對策和多人對策;按得失是否互補分為零和對策和非零和對策;按局中人是否合作分為合作對策和無...
第1章 極小極大定理(對策論)你死我活的對策 策略的對策 兩人零和對策 康科德軍火庫對策 讓他們去猜吧 等 第2章 布勞威爾不動點定理(拓撲學)針和乾草堆 空間的形狀 拓撲學 拓撲等價 不動點遊戲 等 第3章 莫爾斯定理(奇點理論...
3.2.2 兩人零和對策的數學模型和純策略對策的最優解 *3.2.3 鞍點存在的條件 3.3 兩人零和混合策略對策 3.3.1 沒有鞍點的情況 3.3.2 混合策略對策 3.3.3 另一種決定最優混合策略對策的方法 *3.3.4 小敏有多種策略可...
Ⅴ 對策分析技術 第11章 二人有限零和對策 11.1 基本概念 11.2 二人有限零和對策的純策略對策模型 11.3 二人有限零和對策的混合策略對策模型 習題11 第12章 二人有限非零和對策 12.1 二人有限非零和對策問題 12.2 非合作的二人...
該成果可與對策論中“兩人零和矩陣對策必有混合策略解”的定理和數理經濟學中“一般經濟均衡存在定理”相媲美,這兩個定理分別奠定了對策論和數理經濟學的基礎。出版圖書 數學建模 回國後不久,沙基昌就被命任為系統工程與數學系軍事運籌...
第十五章 對策論初步 15.1 對策論的經濟套用 15.2 兩人零和對策及其支付矩陣 15.3 對策期望;純粹策略與固定策略 15.4 極小化極大、鞍點和對策的解 15.5 2×2階的支付矩陣的解 15.6 2×n支付矩陣的圖解 15.7 兩人零和對策...
第九章 對策論 第一節 引言 第二節 兩人有限零和對策 第三節 兩人有限非零和對策 習題九 第十章 網路計畫技術 第一節 網路計畫技術與網路圖 第二節 基於雙代號網路的關鍵路線法 第三節 基於單代號網路的關鍵路線法 第四節 網路...
7.2.2 兩人零和對策的數學模型和純策略對策的最優解 7.2.3 鞍點存在的條件 7.3 兩人零和混合策略對策 7.3.1 沒有鞍點的情況 7.3.2 混合策略對策 7.3.3 另一種決定最優混合策略對策的方法 7.3.4 有多種策略...
第7章 對策論 152 7.1 對策模型的基本要素 153 7.2 矩陣對策(兩人有限零和對策) 155 7.2.1 矩陣對策(兩人有限零和對策)的表示 155 7.2.2 矩陣對策(兩人有限零和對策)的純策略 156 7.2.3 矩陣對策的混合策略 159...
7.2.2 兩人零和對策的數學模型和純策略對策的最優解 7.2.3 鞍點存在的條件 §7.3 兩人零和混合策略對策 7.3.1 沒有鞍點的情況 7.3.2 混合策略對策 7.3.3 另一種決定最優混合策略對策的方法 7.3.4 有多種策略可供選擇...
如果決策者的對方也是人(一個人或一群人)雙方都希望取勝,這類具有競爭性的決策稱為對策或博弈型決策。構成對策問題的三個根本要素是:局中人、策略與一局對策的得失。對策問題一般可分為有限零和兩人對策、陣地對策、連續對策、多人...
第5章對策論模型 5.1引言 5.2兩人有限零和對策 5.3兩人有限零和對策的一般解法 5.4求解中的計算技巧 5.5兩人有限非零和對策 5.6套用實例 習題 第6章網路模型 6.1圖論導引 6.2網路中的流 6.3最短路和最小費用流問題 6.4...
