克魯斯卡爾坐標系

克魯斯卡爾坐標系（或稱作克魯斯卡爾-塞凱賴什坐標系，英文Kruskal coordinates或Kruskal-Szekeres coordinates）是在史瓦西度規下建立的一種坐標系，名稱來自於美國數學物理學家馬丁·克魯斯卡爾（Martin Kruskal）和匈牙利-澳大利亞數學家喬治·塞凱賴什。這種坐標系的優點在於它能夠涵蓋整個時空流形，使得奇點之外的所有點在坐標系中都存在定義，也就是說它能夠將原有的在球坐標系下的史瓦西度規最大限度地推廣到整個時空中。

基本介紹

• 中文名：克魯斯卡爾坐標系
• 外文名：Kruskal-Szekeres coordinates
• 別稱：魯斯卡爾-塞凱賴什坐標系

定義

考慮在球坐標系下的史瓦西度規

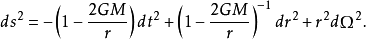
其中

是二維球面的線元。

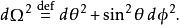
將時間坐標t和徑向坐標 做如下代換：

對於視界外部 r>2GM的區域，

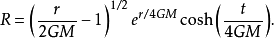
對於視界內部0<r<2GM的區域，

在這些坐標下，史瓦西度規由下式給出：

其中r的定義被隱含在

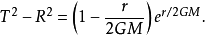
或等價於

其中W是朗伯W函式。

這組由構成的坐標系稱作Kruskal坐標系，有時也稱作Kruskal-Szekeres坐標系。

Kruskal圖

Kruskal坐標的性質

史瓦西黑洞的視界位於r=2GM，此時

的右面為零，從而有。即史瓦西黑洞的視界在T-R平面上是兩條45°的對角線。對於一般的常數r，可以得到。即它們是T-R平面上的一組雙曲線。

對於一般的常數 t，。它們是通過原點的斜率為的直線。注意到當時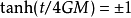，從而等價於的情形。這表明和r=2GM描述的是同一個面。

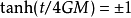
Kruskal圖

Kruskal圖上的每一點都代表了一個二維球面。從圖中可以看到：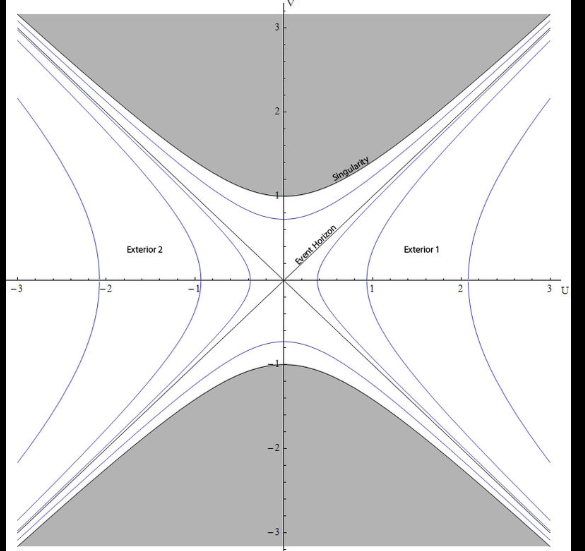

圖1.Kruskal圖

徑向坐標 r可以從正無窮大連續變化到零，中間經過視界r=2GM。其中經過R軸的雙曲線對應著r>2GM的情形，經過T軸的雙曲線對應著 r<2GM的情形，雙曲線的兩條漸近線對應著r=2GM的視界。 r=0對應著黑洞的奇點，而在那以外的部分時間和空間坐標都沒有定義。

時間坐標t可以從負無窮大連續變化到正無窮大，其範圍涵蓋了兩條漸近線（兩條45°的對角線）所夾的包含R軸的部分，即在這範圍內通過原點的所有直線。R軸對應著時間坐標t=0的直線。

在Kruskal坐標下，R具有從負無窮大到正無窮大的連續定義，T也一樣，但兩者在灰色區域仍然沒有定義。

參見

• 史瓦西度規
  
• 彭羅斯圖