基本介紹
- 中文名:伯克霍夫積分
- 外文名:Birkhoff integral
- 所屬學科:數學(測度論)
- 屬性:一種向量值函式的積分
- 提出者:伯克霍夫於1935年提出的
基本介紹















伯克霍夫,G

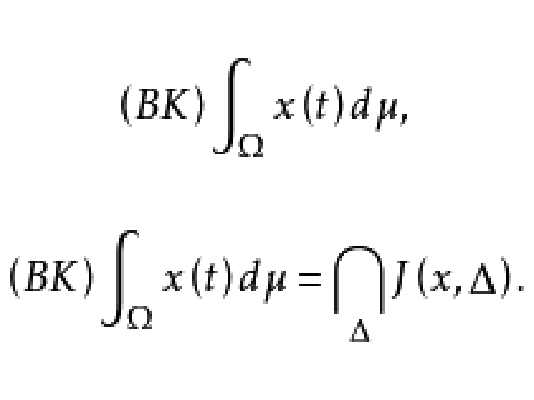
















伯克霍夫積分(Birkhoff integral)是一種向量值函式的積分,是伯克霍夫(G.D.Birkhoff)於1935年提出的.,伯克霍夫積分除富比尼定理外,具有通常勒貝格積分所具有的線性、可列可加性、絕對連續性等性...
《伯克霍夫(Birkhoff)插值及求積公式》是依託中國科學院數學與系統科學研究院,由史應光擔任項目負責人的面上項目。項目摘要 完成論文24篇,已發表12篇,其中發表在《中國科學》上2篇,國外10篇已有2篇為5CI收錄。完全解決了2個圖朗...
伯克霍夫(George David Birkhoff,公元1884年3月21日─公元1944年11月12日)是美國數學家。生於密西根州,卒於麻薩諸塞州的劍橋。1907年在芝加哥大學獲博士學位。先後執教於威斯康辛大學、普林斯頓大學和哈佛大學。人物生平 1884年3月21...
伯克霍夫遍歷定理(Birkhoff ergodic theorem)是遍歷論第一個重要結果。設(X,A,μ,T)是一個保測系統(即T為保測變換),一個可測函式f:X→R代表對系統的一種測量,{f(x),f(Tx),…}給出了軌道{x,Tx,…}的一種信息。
伯克霍夫插值多項式逼近(approximation byBirkhoff interpolation polynomials)是埃爾米特插值多項式逼近的一種推廣。如果在埃爾米特插值過程中放棄在某些點處的某些階導數取值的要求,那么就稱這種插值多項式為伯克霍夫插值多項式。概念 伯克霍夫...
龐加萊-伯克霍夫不動點定理指出閉圓環的任一個保持邊界不動的保面積自同構映射(辛同構)在圓環內部至少有兩個不動點,更一般的保面積的扭曲映射(兩個邊緣轉動方向相反,提升到帶形上看得更清晰)至少有兩個不動點。這個定理來自...
《Birkhoff系統動力學的若干問題研究》是依託蘇州科技大學,由張毅擔任項目負責人的面上項目。項目摘要 伯克霍夫(Birkhoff)力學是哈密頓力學的推廣,哈密頓正則方程經過一般非正則變換就變為伯克霍夫方程.伯克霍夫系統動力學理論是包括哈密...
代數格是伯克霍夫(Birkhoff,G.D.)於1967年引入的,但他並未假設完備性。代數格對契約格的刻畫、格的表示理論和無限維代數理論的研究均有重要作用。伯克霍夫 伯克霍夫是美國數學家。生於普林斯頓,早年在哈佛大學和英國劍橋大學就讀,...
伯克霍夫證明,若R是緊緻度量空間,則在其上定義的動力系統Rt至少包含一個緊緻極小集。當R是緊緻的二維定向流形,在其上定義了C光滑動力系統。若A是Rt的極小集且在R上無處稠密,則A必是休止點或周期軌線。若Ωx中不包含休止點或...
普特南1933年退休,1935年逝世,他的遺孀秉承其遺志,設立了一筆12.5萬美元的普特南基金會,並命他的兩個兒子執行,這件事得到他們全家的摯友、著名美國數學家G.D.伯克霍夫的支持,伯克霍夫認為,再沒有一門學科比數學更易於通過考試...
本項目提出並研究了完整系統、非完整系統和伯克霍夫系統基於阿加瓦爾模型、阿塔納茲庫維奇模型和埃爾-納卜茜模型的分數階變分問題;提出並深入研究了含時滯的完整和非完整系統、伯克霍夫系統的分數階變分問題、變導數分數階伐夫-伯克霍夫...
第四篇專題,包括理論力學的機率問題、打擊運動動力學,運動穩定性、非線性振動、動力學逆問題、力學的變分原理、哈密頓力學、非完整力學、伯克霍夫力學、對稱性與守恆量等10章。前三篇為I冊——基本教程,屬基礎部分;第四篇為Ⅱ冊——...
