仿射坐標變換公式(transformation formula foraffine coordinates)仿射坐標系改變時坐標的變換公式。
基本介紹
- 中文名:仿射坐標變換公式
- 外文名:transformation formula foraffine coordinates
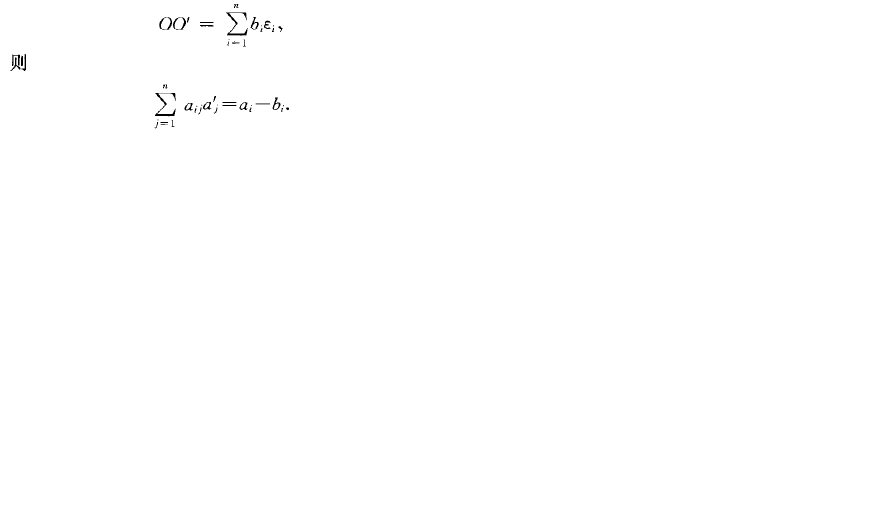
仿射坐標變換公式(transformation formula foraffine coordinates)仿射坐標系改變時坐標的變換公式。
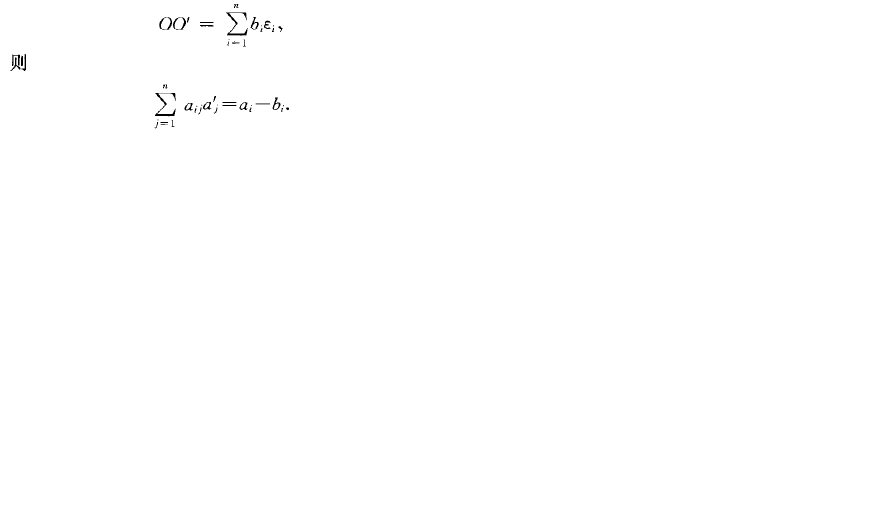
仿射坐標變換公式(transformation formula foraffine coordinates)仿射坐標系改變時坐標的變換公式。定義介紹仿射坐標變換公式(transformation formula fora...
式(1)把點M在坐標系σ下的坐標x,y表示成它在坐標系σ'下的坐標(x',y')的一次多項式,稱為平面上點的仿射坐標變換公式。由於e'₁與e'₂不共線,所以行列式 因此可由方程組(1)解得 式(2)把平面上的點M在坐標系σ'下的坐標(x',y')表示成在坐標系σ下的坐標(x,y)的一次多項式,也稱為平面...
變換公式(1)或(2)右邊是齊次的,在代數上叫做齊次線性變換。因此,以坐標原點作為中心的中心仿射變換的公式是行列式不等於零的齊次線性變換。反之,行列式不等於零的齊次線性變換總表示中心仿射變換(我們還知道它同時可以表示坐標原點不變的仿射坐標變換)。正像仿射坐標變換可以分移軸和坐標原點不變的坐標變換兩步來完成...
叫做變換的模。如果解出方程組(1)的x、y、z,則得到與從平面P'變換到平面P相似的公式,而且在所得的公式中相應的係數是行列式(2)的代數餘子式。我們考慮到平面P與P’的無窮遠直線在仿射變換中也是互相對應的,故可得 ,用非齊次坐標表示此變換,則為 並有行列式 平面P上共線三點M₁、M₂、M₃的...
加上這個條件的原因是:由T的變換公式可以從x和y算出x'和y',但在ae-bd=0時,這並非克萊因 的變換。當ae-bd≠0時,讀者用中學代數中解二元一次方程組的辦法可從T的變換式由x'和y'算出x和y。因而這時T是個變換(一對一的到上映照)。注意,旋轉是一種特殊的仿射變換,此時a=e=cosθ,b=sinθ,d=...
,則稱A為一個n維仿射空間。 時,稱之為仿射平面。由此可見,仿射幾何是一般歐氏幾何的一種擴展。在仿射變換下,直線變為直線,平行直線變為平行直線,但長度與角的大小要改變。這種變換最先由18世紀瑞士數學家歐拉注意到,他在論述解析幾何與微分幾何的坐標變換時涉及到仿射坐標變換問題。19世紀初,德國數學家麥比...
平面直角坐標變換(rectangular coordinates tra-nsformation in the plane)一種常用的坐標變換.指平面上任一點對於兩個直角坐標系(具有相同的長度單位)的坐標之間的對應關係.設任一點M在坐標系x勿中的坐標為((x,婦,在坐標系x' O'夕中的坐標為(xr , yr.平面直角坐標變換公式可直接從仿射坐標變換公...
正投影:為了將向量正投影到一條經過原點的直線,假設 (ux,uy) 是直線方向的單位向量,變換矩陣為:同反射一樣,正投影到一條不經過原點的直線的變換是仿射變換,而不是線性變換。平行投影也是線性變換,也可以用矩陣表示。但是透視投影不是線性變換,必須用齊次坐標表示。變換性質 用矩陣表示線性變換的一個主要動力...
第9章坐標操作方法166 9.1多項式變換方法166 9.1.1一般情況166 9.1.2複數多項式變換173 9.1.3西班牙多項式變換方法175 9.2各種線性坐標操作方法176 9.2.1仿射參量變換方法176 9.2.2一般仿射幾何變換方法177 9.2.3相似變換方法181 9.2.4UKOOAP6地震格網變換方法184 第10章坐標變換188 10.1偏移量—概述...
射影坐標是在射影幾何學中和在研究圖形的純射影性質時,常採用的一種坐標系。它在射影幾何中的作用,就象直角坐標系在歐氏幾何中和仿射坐標系在仿射幾何學中的作用。基本概述 射影 射影是物體在某平面或某空間形成的投影。射影幾何 射影幾何是研究圖形的射影性質,即它們經過射影變換後,依然保持不變的圖形性質的幾何學...
相交於原點的三條不共面的數軸構成空間的仿射坐標系。三條數軸上度量單位相等的仿射坐標系被稱為空間笛卡爾坐標系。三條數軸互相垂直的笛卡爾坐標系被稱為空間笛卡爾直角坐標系,否則被稱為空間笛卡爾斜角坐標系。意義 笛卡爾坐標,它表示了點在空間中的位置,但卻和直角坐標有區別,兩種坐標可以相互轉換。舉個例子:某...
1、仿射變換(affine transfomation)仿射變換變換的公式如下:f(x)=AX=b 其中A是變形矩陣,b是平移矢量。任何一個放射變換可以分解為尺度、伸縮、扭曲、旋轉、平移的組合。2、基本變換 (1)基本幾何變換的定義 對於原圖象f(x,y),坐標變換函式 x’=a(x,y);y’=b(x,y)唯一確定了幾何變換:g(x’,y’...
橢圓旋轉(revolution of an ellipse)是一種平面仿射變換,即將橢圓繞其中心旋轉的平面仿射變換。在平面直角坐標系中,橢圓旋轉τ:(x,y)→(x′,y′)的計算公式為x′=x cos φ-y(a/b)sin φ,y′=x·(b/a)sin φ+ycos φ。基本介紹 平面上把橢圓變成自己的仿射變換用平面上把圓周變成自己的仿射變換...
在此變換以後,弦AB和CD都是圓M的直徑而且四邊形ACBD是圓M內接矩形,PQ也是一條直徑,由對稱性顯然得出投影變換後M為X,Y的中點。又因為變換前後M都是線段PQ的中點,由此可以得出在直線PQ上這個變換是仿射變換,所以變換前M也是XY的中點。例題:如圖7,橢圓的長軸A₁、A₂與x軸平行,短軸B₁B₂在y軸...
雙曲旋轉(revolution of hyperbolic)是一種平面仿射變換,即將雙曲線繞其中心旋轉的平面仿射變換,在平面直角坐標系中,雙曲旋轉的計算公式為:x'=xchφ+y(a/b)shφ,y'=x(b/a)shφ+ychφ。雙曲旋轉的定義和總的描述 下面說明關於把雙曲線變成它自已的非常重要的平面仿射變換。取任意一對相交的...
11.8.2 度量公式144 11.8.3 交點/交線145 11.8.4 插值146 11.8.5 環繞數146 練習146 第十二章 仿射變換和射影變換的與坐標無關的公式151 12.1 三維計算機圖形學中的變換151 12.2 仿射變換和射影變換151 12.3 剛體運動152 12.3.1 平移152 12.3.2 旋轉153 12.3.3 鏡像155 12.4 放縮156 12....
5 空間直角坐標變換 5.1 平移 5.2 旋轉 5.3 一般的坐標變換 6 二次曲面的分類定理 問題與練習 第六章 變換群與幾何學 1 變換群 1.1 點變換 1.2 變換群 2 正交變換與歐氏幾何 2.1 基本概念 2.2 代數表示式 2.3 正交變換群 3 仿射變換與仿射幾何 3.1 平面上的仿射坐標系與仿射變換 3.2 仿射...
2.1.4 一維射影映射的坐標表示 習題2.1 §2.2 一維射影變換 2.2.1 直線上的射影變換 2.2.2 對合 習題2.2 §2.3 直射 2.3.1 直射映射 2.3.2 直射變換 2.3.3 調和同調變換 2.3.4 直射與坐標變換的關係 習題2.3 §2.4 歐氏平面上的仿射變換 習題2.4 第三章 二次曲線的射影理論 §3....
高等幾何》教材中的習題;其二是本書的最後:解題指導與答案。圖書目錄 第一部分 學習指導及習題 第一章 仿射坐標與仿射變換 1 透視仿射對應 2 仿射對應與仿射變換 3 仿射坐標 4 仿射性質 習題 5 本章小結 綜合練習題 第二章 射影平面 1 射影直線和射影平面 習題 2 齊次坐標 習題 3 對偶原理 ...
Ⅲ.用直角坐標表示度量性質的基本公式∥57 Ⅳ.用廣義笛氏坐標表示度量性質的基本公式∥74 Ⅴ.各種坐標系∥83 第三章 笛氏坐標的變換,運動和仿射變換∥89 Ⅰ.笛氏坐標變換的一般公式∥89 Ⅱ.坐標變換的最重要特例∥100 Ⅲ.運動和仿射變換∥114 第四章 平曲線的方程.平面上的直線∥129 Ⅰ.平曲線的分析表示法...
§5 空間直角坐標變換 5.1 平移 5.2 旋轉 5.3 一般的坐標變換 §6 二次曲面的分類定理 問題與練習 第六章 變換群與幾何學 §1 變換群 1.1 點變換 1.2 變換群 §2 正交變換與歐氏幾何 2.1 基本概念 2.2 代數表示式 2.3 正交變換群 §3 仿射變換與仿射幾何 3.1 平面上的仿射坐標系與仿射變換...
例如,假若,我們用坐標向量(coordinate vector來表示 與 。那么,線性函式可以表達為 其中, 是矩陣。套用 仿射變換是指一個向量空間進行一次線性變換並接上一個平移,變換為另一個向量空間。一個對向量 平移 ,與旋轉放大縮小 的仿射映射為 上式在齊次坐標上,等價於下面的式子 在分形的研究里,收縮平移...
首先用SURF算法提取待檢測圖像的特徵點和特徵向量,找出匹配特徵點後,計算出仿射變換參數並消除錯配,再根據仿射變換計算區域關聯圖定位複製一移動區域。最後,根據複製—移動區域的塊偽影特徵矩陣因子區分被複製區域和篡改區域。步驟1:SURF 特徵點提取與匹配。由於SURF算法提取特徵點利用的是圖像的灰度信息,因此,首先...
9.3 曲線的曲率 撓率 弗雷耐公式 9.4 特殊的空間曲線 9.5 曲面的表示 切平面 參數變換 9.6 曲面的第一基本形式 9.7 曲面上曲線的法曲率 曲面的第二基本形式 習題 第10章 平面正交變換 仿射變換 射影變換 10.1 平面正交變換 10.2 平面的仿射變換 10.3 射影平面與齊次坐標 10.4 射影映射和射影變換 習...
首先是莫比烏斯創建一種齊次坐標系,把變換分為全等,相似,仿射,直射等類型,給出線束中四條線交比的度量公式等。接著,普呂克引進丁另一種齊次坐標系,得到了平面上無窮遠線的方程,無窮遠圓點的坐標。他還引進了線坐標概念,於是從代數觀點就自然得到了對偶原理,並得到了關於一般線素曲線的一些概念。在19世紀前...
公式 使用Mode 7圖形的平面紋理地圖,是由螢幕坐標到背景坐標的2D仿射變換而轉換成,a、b、c和d是轉換係數;x和y是螢幕偏移;x₀和y₀是初始偏移;x'和y'是轉換坐標。全部運算都為16位有符號定點數,而全部偏移僅限制在13位。小數點位於7和8位之間。仿射變換僅允許位移、縮放和剪下效果。許多遊戲通過逐...
5.3.1 仿射聯絡的定義和性質 5.3.2 黎曼聯絡 5.4 平行移動測地線 5.4.1 預先的觀察 5.4.2 平行移動的方程 5.4.3 測地線 5.5 曲率張量 5.5.1 預先的觀察 5.5.2 曲率張量的坐標定義 5.5.3 曲率張量的不變的定義 5.5.4 黎曼曲率張量的代數性質 5.5.5 黎曼曲率張量的某些套用 ...
SIFT(尺度不變特徵變換匹配) 算法是一種基於不變數技術的特徵描述算法,可在空間域和尺度域上同時進行特徵點的計算和提取,所提取的圖像局部特徵不僅對平移、縮放、旋轉變換具有不變性,而且對視角變化、光照變化、仿射變形、加性噪聲等影響也具有較高的容忍度,能夠正確地提取尺度和視角變化較大的圖像序列中的特徵點...
5.1.1 移軸變換 5.1.2 轉軸變換 5.1.3 正交條件 5.1.4 一般坐標變換公式 5.1.5 向量的坐標變換 5.1.6 以三垂直平面為新坐標系坐標平面的坐標變換 5.2 點變換 5.2.1 點變換的定義 5.2.2 點的平移 5.2.3 點的旋轉 5.2.4 剛體運動 5.2.5 正交變換 5.2.6 仿射變換 *5.3 坐標變換...
