中心仿射變換群是仿射變換群的子群,即平面上以同一點為中心的中心仿射變換的全體構成一個群,稱為中心仿射變換群。
基本介紹
- 中文名:中心仿射變換群
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
- 相關概念:中心仿射變換
基本介紹




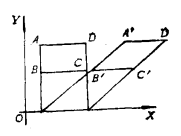
中心仿射群



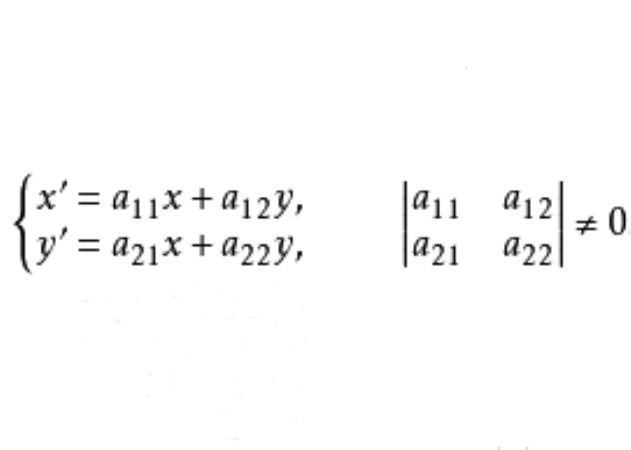
中心仿射變換群是仿射變換群的子群,即平面上以同一點為中心的中心仿射變換的全體構成一個群,稱為中心仿射變換群。








中心仿射變換群是仿射變換群的子群,即平面上以同一點為中心的中心仿射變換的全體構成一個群,稱為中心仿射變換群。基本介紹定義 保持原點不變的仿射變換叫做中心仿射變換,它的坐標表示是前面講過的向X軸或向Y軸的壓縮是中心仿射變換...
中心仿射群 仿射幾何是由線性變換群 制約的。這種變換可以認為是 和平移 複合而成的。上面像T的這種變換稱為齊次仿射變換或中心仿射變換,這種變換構成的集稱為齊次仿射群或中心仿射群。用“中心的"這個形容詞是因為原點或“中心”在這種變換下不變(用x=0,y=0代入即得)。式中a,b,d,e是實參數,並且滿足ae-...
稱之為射影變換群,仿射變換群、相似變換群、正交變換群都是它的子群。仿射變換 仿射變換是射影變換的特殊情況,當定義中心射影的線束為互相平行的直線時,變換稱為仿射變換,由於線束中的直線互相平行,顯然,仿射變換保持交比不變。相關知識 射影平面 射影平面就是2維射影空間。它可以視為平面添上一條無窮遠直線。
仿射變換 由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交變換、相似變換、仿射變換都保持共線三點的單比不變,必然保持共線四點的交比不變,所以這些變換都是射影變換。如果平面上點場的點建立了一個一一...
這種觀點突出了變換群在研討幾何中的地位,後來簡稱為《埃爾朗根綱領》。因此,仿射微分幾何的根本目的是研究子流形在仿射變換群下的不變性質。本項目研究了中心仿射變換下,仿射空間中的超曲面和餘二維子流形的微分不變數和積分不變數。首先,本項目研究了3 維仿射空間中的仿射旋轉曲面在中心仿射變換下的不變性質。...
射影幾何中有意義的性質均與新的變換概念有關,此一變換比透過變換矩陣或平移(仿射變換)表示的變換更為基礎。對幾何學家來說,第一個問題是要找到一個足以描述這個新的想法的幾何語言。不可能在射影幾何內談論角,如同在歐氏幾何內談論一般,因為角並不是個在射影變換下不變的概念,如在透視圖中所清楚看到的一般...
有限個點總存在幾何中心,可以通過計算這些點的每個坐標分量的算術平均值得到。這箇中心是空間中一點到這有限個點距離的平方和的惟一最小值點。點集的幾何中心在仿射變換下保持不變。判斷位置 判斷形心的位置:當截面具有兩個對稱軸時,二者的交點就是該截面的形心。據此,可以很方便的確定圓形、圓環形、正方形。形心...
S上關於U的自同構變換的全體構成一個變換群,稱它為關於U的自同構群。在變換中保持不變的這個圖形U稱為絕對形。例如,在射影平面上取一條直線作無窮遠直線,則在射影平面上保持無窮遠直線不變的自同構射影變換構成一個變換群,它是關於無窮遠直線的自同構群,同時它也是二維射影變換群的子群,即仿射變換群。
的自同構之全體構成射影變換群的子群,即仿射變換群。又如,射影變換群中關於兩個圓點所成集合的自同構之全體構成射影變換群的子群,即相似變換群。在射影平面上任取一條常態實二階曲線 ,且取 的一個自配極三點形作為坐標三點形時,它的方程是 ,則射影變換群中關於 的自同構之全體也構成射影變換群的子群.我...
按照變換群的觀點,幾何學可以這樣分類:研究射影變換群、仿射變換群、相似變換群、正交變換群下不變性質和不變數的幾何學分別是射影幾何學、仿射幾何學、拋物幾何學、歐氏幾何學.正交變換群也稱為運動群,歐氏幾何學的主要內容就是研究運動群下不變性質和不變數的幾何學.近代發展很快、套用越來越廣的一門學科——...
《高等學校教材:解析幾何》共分為六章,詳盡地講述了向量代數、空間坐標系、平面和直線、幾種常見的曲面和曲線、二次曲面的一般理論、變換群與幾何學的基本理論。部分集中、部分分散地介紹了仿射幾何、射影幾何中一些要點,介紹了解析幾何的基本方法與技巧,介紹了建立幾何學的另外一種方法——克萊因變換群的思想,並...
它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若是一個已知的向量,是空間中一點,平移。將同一點平移兩次,結果可用一次平移表示,即,因此所有平移的集是一個群,稱為平移群。這個群和空間同構,又是歐幾里德群E(n)的正規子群...
第四章 仿射幾何與歐氏幾何 §4.1 仿射幾何 4.1.1 仿射平面 4.1.2 仿射變換 習題4.1 §4.2 二次曲線的仿射理論 4.2.1 仿射二次曲線 4.2.2 仿射二次曲線的中心,直徑與漸近線 習題4.2 §4.3 歐氏幾何 4.3.1 虛點、虛直線 4.3.2 歐氏變換與歐氏幾何 4.3.3 歐氏二次曲線 習題4.3 §4...
影像對準是指找出兩張影像之間的變換關係,如平移、旋轉、縮放,經過變換之後使兩張影像中相同的部分可以重疊。影像之間的變換關係可以用一個矩陣來表示,所要求得的矩陣的未知數數量越多,代表兩影像之間的關係越複雜、越難對準。舉例而言,平移矩陣有兩個未知數,仿射變換矩陣有六個未知數,而一般化的投影矩陣則有...
5.3 一般的坐標變換 §6 二次曲面的分類定理 問題與練習 第六章 變換群與幾何學 §1 變換群 1.1 點變換 1.2 變換群 §2 正交變換與歐氏幾何 2.1 基本概念 2.2 代數表示式 2.3 正交變換群 §3 仿射變換與仿射幾何 3.1 平面上的仿射坐標系與仿射變換 3.2 仿射變換的基本性質 3.3 仿射變換群與...
它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若 是一個已知的向量,是空間中一點,平移 。將同一點平移兩次,結果可用一次平移表示,即 ,因此所有平移的集是一個群,稱為平移群。這個群和空間同構,又是歐幾里德群E(n)的正規...
例1 下列概念中哪些是仿射的,哪些是相似而非仿射的,哪些只是度量的?為什麼?(1)垂直;(2)線段中點;(3)中心對稱和對稱中心;(4)軸對稱;(5)三角形及其重心;(6)平行四邊形;(7)梯形;(8)二次曲線;(9)焦點、準線、離心率;(10)焦參數;(11)圓。解: 由仿射變換保持簡比不變易知(2)是仿射概念,...
射影空間具有射影變換群,仿射空間與共形空間分別具有仿射變換群與共形變換群等等。這樣就用變換群對已有的幾何學進行了分類。這些幾何學中所研究的對象是在相應變換群下不變的性質。這種用群論統一幾何學的思想把幾何學與李群結合起來了。在《埃爾朗根綱領》發表後的半個世紀內,它成了幾何學的指導原理,推動了幾何學...
本卷首先給出了若干必要的預備知識,主要包括微分流形、張量代數與張量分析、Lie群和纖維叢等.本卷的中心內容是聯絡理論,不僅論述了一般聯絡理論,還具體講述了線性聯絡、仿射聯絡、黎曼聯絡等。然後講述了曲率形式和空間形式以及各種空間變換.此外,本卷還給出了7個附錄和11個注釋,分別介紹了若干備查知識和歷史背景...
1 仿射坐標系與仿射平面 1.1 平行射影 1.2 仿射坐標系與仿射平面 2 仿射變換的相關問題 2.1 仿射變換的代數表達式 2.2 關於仿射變換的確定及其重要定理 2.3 仿射平面上直線的幾個常用結論 2.4 幾種重要的仿射變換 2.5 仿射性質 練習4 第5章 從仿射平面到射影平面 1 擴大的仿射平面 1.1 中心射影和...
1仿射坐標系與仿射平面 1.1平行射影 1.2仿射坐標系與仿射平面 2仿射變換的相關問題 2.1仿射變換的代數表達式 2.2關於仿射變換的確定及其重要定理 2.3仿射平面上直線的幾個常用結論 2.4幾種重要的仿射變換 2.5仿射性質 練習5 第6章從仿射平面到射影平面 1擴大的仿射平面 1.1中心射影和無窮遠元素 1.2射影...
②建立整體映射函式:根據圖像的幾何畸變性質及地面控制點的多少來確定校正數學模型,建立起圖像與地圖之間的空間變換關係,如多項式方法、仿射變換方法等。③重採樣內插:為了使校正後的輸出圖像像元與輸入的未校正圖像相對應,根據確定的校正公式,對輸入圖像的數據重新排列。在重採樣中,由於所計算的對應位置的坐標不是...
§4.3極點與極線,配極變換 §4.4二階曲線的射影分類 §4.5二階曲線上的射影變換與對合 §4.6二次曲線束 §4.7二次曲線的仿射理論 §4.8二次曲線的度量理論 習題 練習題 第五章變換群與幾何學 內容提要 §5.1變換群的概念 §5.2二維射影群及其子群 §5.3變換群與幾何學 習題 練習題 第六章...
圓是特殊的橢圓,即圓通過仿射變換可以變成橢圓,所以先研究圓。(1)兩條動直線交點為圓上的某個定點 如圖,AB是圓的一條直徑,從圓上的定點A引出兩條弦AP、AQ。若PQ過AB上的定點M,則kk為定值。反之,若kk為定值,則PQ經過定點M。利用三角形面積公式,。當AB為x軸時,tanαtanβ恰好就是kk。所以當M為...
3.5 幾何變換法 3.6 同一法與反證法 練習十七 3.7 向量法與複數法 3.8 面積方法,構造法等 練習十八 第四章 解平面幾何題的其他方法 4.1 仿射變換與用仿射法解平幾題 4.2 射影變換與用射影法解平幾題 練習十九 4.3 反演變換與用反演法解平幾題 4.4 向量法與複數法的一些拓展 練習二十 4.5 三角...
本卷首先給出了若干必要的預備知識,主要包括微分流形、張量代數與張量分析、Lie群和纖維叢等.本卷的中心內容是聯絡理論,不僅論述了一般聯絡理論,還具體講述了線性聯絡、仿射聯絡、黎曼聯絡等。然後講述了曲率形式和空間形式以及各種空間變換.此外,本卷還給出了7個附錄和11個注釋,分別介紹了若干備查知識和歷史背景...
4.1 坐標變換 4.1.1 旋轉變換 4.1.2 齊次變換 4.2 位移運算元與坐標變換 4.2.1 位移運算元 4.2.2 坐標變換與位移運算元的關係 4.3 一般運動的仿射變換及其空間結構與群表示 4.4 旋轉運算元、旋轉群so(3)與指數映射 4.4.1 群公理與李群 4.4.2 旋轉群 4.4.3 euler-rodrigues方程與so(3)到so(3)的...
對於常態分配參數空間的仿射變換,正確的哈爾度量是Jeffreys先驗度量。不幸的是,即使是正確的Haar措施有時也會導致無用的先驗,不能被推薦用於實際使用,就像其他方法來構造先前的避免主觀信息的措施 在統計學中,哈爾度量的另一種用法是條件推理,即統計數據的抽樣分布取決於數據的另一個統計數據。在不變數理論條件...
