基本介紹
- 中文名:形心
- 外文名:centroid
- 概念:幾何中心
- 性質:針對抽象幾何體而言的
- 特點:質心和形心重合
- 套用學科:幾何學
定義
判斷位置
 形心
形心性質




三角形的中心
四面體的中心


多邊形的中心

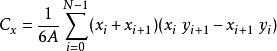

有限點集中心



面積中心




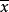


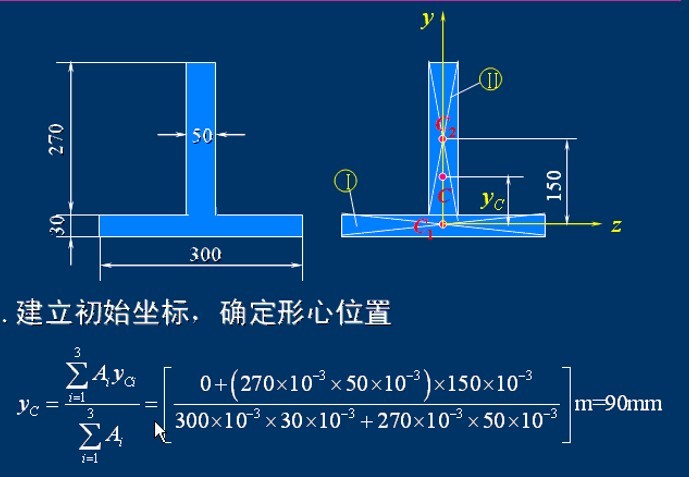
 形心
形心






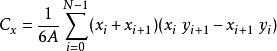








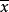


面的形心就是截面圖形的幾何中心,質心是針對實物體而言的,而形心是針對抽象幾何體而言的,對於密度均勻的實物體,質心和形心重合。n 維空間中一個對象X的幾何中心或...
靴形心並不是一種疾病,而是心臟的一種形態改變。靴形心是影像學上的詞,是描述胸片上心外形的。靴形心是主動脈型心影,是指左心室擴大時胸片上表現為心尖圓隆下...
形心因素分析(centroid factor analysis)亦稱“形心法”、“重心法”。是因素分析的一種方法。群因素分析的推廣。美國心理學家瑟斯頓創立。電子計算機出現之前最常用...
來源材料力學中表示某一構件截面幾何性質的軸線。定義在構件某一截面上,使慣性積等於零的一對正交坐標軸稱為慣性主軸,簡稱主軸,如果主軸通過平面圖形的形心,則稱...
內容簡介“恆星群形心”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。 中文...
加權形心單純形法weighted centroid simplex mcthad在改進單純形法的摹礎上發展起來的一種單純形最佳化方法。由除回響值最差的頂點W以外的其餘各單純形頂點的回響值...
控制加權形心單純形法(}r}ntrnlled weighted }entrflid sim- Alex method)在加權形心單純形法的基礎上引人控制條件 的一種單純形最佳化方法。...
其中Iy, Iz是截面對坐標軸的慣性矩,Iyz是截面對坐標軸的慣性積;Iyc, Izc是截面對形心軸的慣性矩,Iyz是截面對形心軸的慣性積;a,b分別指的是形心距y軸、z...
靴形心,是指心臟濁音界向左下擴大,心腰部由鈍角變為近似直角,使心濁音界呈靴型,因其常見於主動脈關閉不全,也可見於主動脈瓣狹窄,又稱為主動脈型心,也可見於...
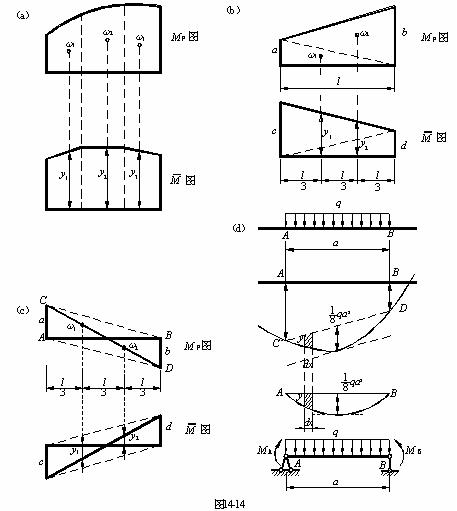
(3)彎矩圖面積ω與對應形心標距y若在桿件的同側則乘積取正號,異側則取負號。圖乘法套用舉例 編輯 如圖所示,設等截面直桿AB段上的兩個彎矩圖中, 圖為一段...
平面圖形的面積A與其形心到某一坐標軸的距離的乘積稱為平面圖形對該軸的靜矩。一般用S來表示。靜距的量綱為長度的3次方,也就是L3。有時候又稱為截面面積矩。...
其大小為該截面截取的構件部分上所有外力對該截面形心矩的代數和,其正負約定為是構件下凹為正,上凸為負(正負區分標準是構件上部受壓為正,下部受壓為負;反之構件...
彎曲中心(bending center)亦稱“剪下中心”。是指梁在兩個形心主慣性平面(各截面形心主軸所組成的平面)內分別發生彎曲時,橫截面上相應的兩個剪力作用線的交點。如...
五心說”為太極拳理論之一。五心是體心、形心、意心、神心、天心之分合調運以及接換斷續之竅。...
靜面矩構件截面的幾何性質,如靜矩、形心、軸慣性矩、極慣性矩、慣性積和主慣性軸位置等,對構件承力性能產生影響,常被用於分析桿件的彎曲、扭轉和剪下等問題。...
浮心(center of buoyancy)是指浮體或潛體水下部分體積的形心。當浮體方位在鉛直面內發生偏轉時,其水下部分的體積雖保持不變,但其形狀卻發生變化,因而浮心的...
