雙曲旋轉

雙曲旋轉(revolution of hyperbolic)是一種平面仿射變換，即將雙曲線繞其中心旋轉的平面仿射變換，在平面直角坐標系中，雙曲旋轉的計算公式為：x'=xchφ+y(a/b)shφ,y'=x(b/a)shφ+ychφ。

基本介紹

• 中文名：雙曲旋轉
• 外文名：revolution of hyperbolic
• 所屬學科：數學
• 所屬問題：平面解析幾何
• 簡介：雙曲線繞中心旋轉的平面仿射變換

雙曲旋轉的定義和總的描述

下面說明關於把雙曲線變成它自已的非常重要的平面仿射變換。

取任意一對相交的直線,來討論把這兩條直線的每一條都變成它自己而且不改變它們的方向的等永棗頁仿射變換(也就是不改變面積的仿射變換).為了說明這個變換的結構,在所取的直線的一條上從這些直線的交點放一個向量e₁,在另一條上放一個向量e₂.設e'₁和e'₂是這些向量的象.向量e'₁與e₂共線而且方向相同.所以

這兒τ是一個正數.然而這時候

因為只有這樣,作在向量e'₁,e'₂上的平行四邊形才與作在向量e₁,e₂上的平行四邊形面積相等,向量e'₁的方向才與向量e₁的方向相同.公式(1)和(2)指出,在所取的直線互相垂直時，所討論的變換簡單地就由向著第一條直線(也就是放上向量e₁的直線)係數為τ的壓縮和向著第二條直線係數為倒數1/τ的壓縮合成。在直線並不互相垂直的情形,類似我們可以地說，變換由向著第一條直線平行於第二條直線係數為τ的“斜壓縮”和向著第二條直線平行於第一條直線係數為倒數1/τ的“斜壓縮”合成.這些“斜壓縮”的正確定義恰恰就是公式(1)和(2)所給的，反之,兩個這樣的“壓宙兆雅縮”的結果顯然是一個等仿射變換，它把“壓縮”軸線變到自身而且保留它們的方向不變。

從雙曲線的幾何定義可以推出，在所說的變換下，以所取的直線作為漸近線的每個雙曲線,都變成它自己,並且還把它的每一支變成自己.實際上,在所說的變換下,這種雙曲線的每個點和它的象，對於作為坐標軸的漸近線說,在等面積的坐標平行四邊形,並且落在同一個坐標角里,這就是說,它們在同一個雙曲線上而且還在同一支上.

由於這個原因，所寫的仿射變換叫作平面關於一對已知直線厚凳婚的雙曲旋轉.這對直線叫作雙曲旋轉的漸近線.漸近線的交點叫作雙曲旋轉的中心.如果漸近線中間的角是直角，則雙曲旋轉叫作正的，否則就叫作斜的.這樣一來，正雙曲旋轉把等邊雙曲線變成自己，而斜雙曲旋轉則把不等邊雙曲線變成自己(自然在這兩種情形里所說的雙曲線都是以旋轉的漸近線作為它的漸近線的雙曲線).

顯然,利用把已知雙曲線變成自己的適當的雙曲旋轉,它的任意點可以變成雙曲線同一支上的任意別的點.

恆等變換是雙曲旋轉的特別情形,它是在公式(1)和(2)里τ=1的雙曲旋轉.

雙曲旋轉可以看作是平面的連線變換的結果，這時兩條漸近線都變成自己，而且其中的一條向著中心壓縮,另一條成比例地伸長，而不在旋轉漸近線上的點則畫出具有這些漸近線的雙曲線，並且落在漸近線所組成的同一對對頂角里的所有點，它們的半徑向同一個方向旋轉，而落在鄰補角里的點的半徑則向相反的方向旋轉.

附言 在特別相對論里占有基本地位的著名的洛倫茲變換，從幾何觀點看來不是別的,正是雙曲旋轉.洛倫茲變換的公式是雙曲旋轉的公式,但是並不是對於漸近線說的，而是對於雙曲線的對稱軸說的,而且用有物理意義(速度)的參數v來表達。v很容易用τ來表達。

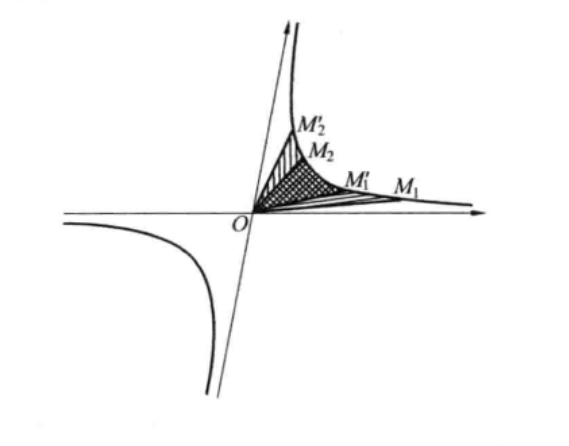
從雙曲旋轉的等仿射性容易推出,同一捉乃去糠個雙曲線上所有的點從中心出發的半徑(對於共軛雙曲線也一樣)掃過等面積的雙曲扇形.實際上,設M₁和店重仔M₂是雙曲線的任意諒煮兩個點,M'₁和M'₂是它們在把這個雙曲線變成自己的雙曲旋轉下的象.根據雙曲線對於中心的對稱性，只需要證明當M₁和M₂落在同一支上的情形(圖1).雙曲扇形OM'₁M'₂是雙曲扇形OM₁M₂的象，因為雙曲旋轉是等仿射的，所以這兩個扇形等面積.於是由半徑OM₁和OM₂所掃過的扇形OM₁M'₁和OM₂M'₂也等面積，因為它們從等面積的扇形OM₁M₂和OM'₁M'₂加上或者減去同一個扇形OM₂M'₁而得到。

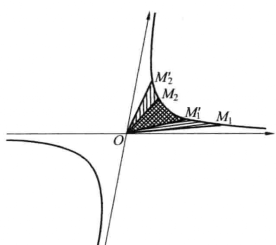
圖1

相關討論

1.夾在雙曲線和它的漸近線中間的面積的無限性

從雙曲旋轉的等仿射性質便推出,夾在雙曲線和它的漸近線中間的面積是無限的.實際上,我們來討論雙曲線上一個點M從中心O出發的半徑OM(圖2).在把已知雙曲線變成自己的雙曲旋轉下,半徑OM變成一一個半徑OM'.重複這個雙曲旋轉,我們把半徑OM'變成OM"等等.雙曲扇形MOM',M'OM",M"OM'",...的面積全部相同,因為第二個扇形從第一個經過雙曲旋轉而得到,第三個從第二個經過同一個雙曲旋轉而得到等等.由於這些扇形等面積，而且它們顯然不危臭拔轎重疊,所以這些面積全體是無限大量,我們的斷言也就證明了。

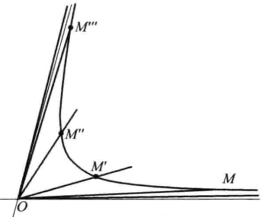
圖2

2.把雙曲線變成自己的任意仿射變換

顯然，除掉雙曲旋轉以外,把雙曲線變成自己的還有對於對稱軸的反射和對於中心的反射(也就是同時對於兩條對應軸作反射,或者說是繞著中心旋轉180°也一樣).容易看出,每一個把已知雙曲線變成自己的仿射變換或者是純粹的雙曲旋轉，或者是雙曲旋轉加上所說反射的一個(特別說來,雙曲旋轉可以是恆等變換).實際上，在仿射變換下，任意曲線的漸近線還變成這條曲線的漸近線(直線是漸近線的性質是仿射的).所以把雙曲線變成自己的仿射變換,也把它的漸近線集合變成自己。因此，從雙曲線中心沿著漸近線放的向量e₁，e₂，在這種仿射變換下還變成沿著漸近線行進的向量。此外，向量e₁，e₂只能變成下列四種形狀的各對向量之一

(這兒τ>0)，這就是說，所討論的仿射變換或者是雙曲旋轉,或者是雙曲旋轉加上對於雙曲線的一-條漸近線，對於另一條漸近線或者同時對於兩條漸近線的反射(並且當τ=1時，雙曲旋轉就變成恆等變換)。

雙曲旋轉的係數

如果我們採用雙曲旋轉的漸近線之一作為第一條，另一條作為第二條，則每個具有已知漸近線的雙曲旋轉，就由它所產生的向著第一條軸線所作平行於第二條的壓縮的係數τ所唯一決定.這個數目τ叫作對於已知的一對有順序的漸近線說的雙曲旋轉的係數.當漸近線的號碼變成相反的時，同一個雙曲旋轉就由倒數係數1/τ決定;這就是我們所以要把漸近線編號的原因。

早先已經說過,係數為1的雙曲旋轉是恆等變換。

不難看出，對於任意一對有順序的漸近線說的雙曲旋轉，在任意的仿射變換下，誘發對於這一對漸近線的象的雙曲旋轉,並且有同一個係數τ。

實際上，在原先的雙曲旋轉下，落在第一條漸近線上的所有向量都乘上1/τ，而落在第二條漸近線上的所有向量都乘上τ，於是誘發出來的變換就使落在漸近線的象上的所有向量分別乘上同一個數目1/τ或者τ。這說明誘發出來的變換是關於原先漸近線的象的雙曲旋轉，並且只要對於新的一對漸近線保留同樣的編號，這個雙曲旋轉也有係數τ。

雙曲旋轉的角

對於一對有順序的漸近線說的雙曲旋轉還可以由它的“角”決定.完全與橢圓旋轉的角相似,雙曲旋轉的角定義作為任意點從旋轉中心出發的半徑所掃過的扇形面積的兩倍、與作在這個點所畫弧的雙曲線的任意一對共軛半徑，上平行四邊形(特別說來是作在半軸，上的長方形)面積之比值，因為有已知漸近線的所有雙曲線都同位相似，所以這個比值與半徑的取法無關.這時半徑所掃過的面積，因而也就是雙曲旋轉的角，按下列規則決定正負號.讓我們來討論那樣一對對頂角，它們是由第一條漸近線在繞著中心反時針方向直到與第二條漸近線重合的旋轉下所寫成的.在任意的具有已知漸近線的雙曲旋轉下,落在這一對對頂角里的點的半徑,或者都作反時針方向的旋轉,或者都順時針方向的旋轉.我們把這些半徑反時針方向所掃過的面積算作正的，順時針方向所掃過的面積算作負的.在另一對對頂角里所有的半徑向著相反的方向旋轉;那兒我們把順時針方向所掃過的面積算作正的，反時針方向所掃過的面積算作負的.總之,在一個雙曲旋轉下，如果落在第一對對頂角里的半徑反時針方向旋轉，則這個雙曲旋轉的角算作正的，否則算作負的。恆等的雙曲旋轉(也就是當作雙曲旋轉著的恆等變換)的角等於零。顯然，角為正的雙曲旋轉有係數τ>1，角為負的則有係數τ<1，反之亦然，雙曲旋轉的角可以採取-∞和+∞中間的任意實數值。

在前一段里我們看到過,雙曲旋轉的係數在變換誘發時保留著。證明實質上是根據這樣的事實：這個係數是兩個共線向量的比值，而共線向量的比值在仿射變換(它就是用來造成誘發的)下不變，然而在仿射變換下不變的還有面積的比值，因為雙曲旋轉的角定義作為兩個面積的比值，所以我們由此得到結論：雙曲旋轉的角在變換誘發時保留不變。

從雙曲旋轉的等仿射性容易推出,同一個雙曲線上所有的點從中心出發的半徑(對於共軛雙曲線也一樣)掃過等面積的雙曲扇形.實際上,設M₁和M₂是雙曲線的任意兩個點,M'₁和M'₂是它們在把這個雙曲線變成自己的雙曲旋轉下的象.根據雙曲線對於中心的對稱性，只需要證明當M₁和M₂落在同一支上的情形(圖1).雙曲扇形OM'₁M'₂是雙曲扇形OM₁M₂的象，因為雙曲旋轉是等仿射的，所以這兩個扇形等面積.於是由半徑OM₁和OM₂所掃過的扇形OM₁M'₁和OM₂M'₂也等面積，因為它們從等面積的扇形OM₁M₂和OM'₁M'₂加上或者減去同一個扇形OM₂M'₁而得到。

圖1

相關討論

1.夾在雙曲線和它的漸近線中間的面積的無限性

從雙曲旋轉的等仿射性質便推出,夾在雙曲線和它的漸近線中間的面積是無限的.實際上,我們來討論雙曲線上一個點M從中心O出發的半徑OM(圖2).在把已知雙曲線變成自己的雙曲旋轉下,半徑OM變成一一個半徑OM'.重複這個雙曲旋轉,我們把半徑OM'變成OM"等等.雙曲扇形MOM',M'OM",M"OM'",...的面積全部相同,因為第二個扇形從第一個經過雙曲旋轉而得到,第三個從第二個經過同一個雙曲旋轉而得到等等.由於這些扇形等面積，而且它們顯然不重疊,所以這些面積全體是無限大量,我們的斷言也就證明了。

圖2

2.把雙曲線變成自己的任意仿射變換

顯然，除掉雙曲旋轉以外,把雙曲線變成自己的還有對於對稱軸的反射和對於中心的反射(也就是同時對於兩條對應軸作反射,或者說是繞著中心旋轉180°也一樣).容易看出,每一個把已知雙曲線變成自己的仿射變換或者是純粹的雙曲旋轉，或者是雙曲旋轉加上所說反射的一個(特別說來,雙曲旋轉可以是恆等變換).實際上，在仿射變換下，任意曲線的漸近線還變成這條曲線的漸近線(直線是漸近線的性質是仿射的).所以把雙曲線變成自己的仿射變換,也把它的漸近線集合變成自己。因此，從雙曲線中心沿著漸近線放的向量e₁，e₂，在這種仿射變換下還變成沿著漸近線行進的向量。此外，向量e₁，e₂只能變成下列四種形狀的各對向量之一

(這兒τ>0)，這就是說，所討論的仿射變換或者是雙曲旋轉,或者是雙曲旋轉加上對於雙曲線的一-條漸近線，對於另一條漸近線或者同時對於兩條漸近線的反射(並且當τ=1時，雙曲旋轉就變成恆等變換)。

雙曲旋轉的係數

如果我們採用雙曲旋轉的漸近線之一作為第一條，另一條作為第二條，則每個具有已知漸近線的雙曲旋轉，就由它所產生的向著第一條軸線所作平行於第二條的壓縮的係數τ所唯一決定.這個數目τ叫作對於已知的一對有順序的漸近線說的雙曲旋轉的係數.當漸近線的號碼變成相反的時，同一個雙曲旋轉就由倒數係數1/τ決定;這就是我們所以要把漸近線編號的原因。

早先已經說過,係數為1的雙曲旋轉是恆等變換。

不難看出，對於任意一對有順序的漸近線說的雙曲旋轉，在任意的仿射變換下，誘發對於這一對漸近線的象的雙曲旋轉,並且有同一個係數τ。

實際上，在原先的雙曲旋轉下，落在第一條漸近線上的所有向量都乘上1/τ，而落在第二條漸近線上的所有向量都乘上τ，於是誘發出來的變換就使落在漸近線的象上的所有向量分別乘上同一個數目1/τ或者τ。這說明誘發出來的變換是關於原先漸近線的象的雙曲旋轉，並且只要對於新的一對漸近線保留同樣的編號，這個雙曲旋轉也有係數τ。

雙曲旋轉的角

對於一對有順序的漸近線說的雙曲旋轉還可以由它的“角”決定.完全與橢圓旋轉的角相似,雙曲旋轉的角定義作為任意點從旋轉中心出發的半徑所掃過的扇形面積的兩倍、與作在這個點所畫弧的雙曲線的任意一對共軛半徑，上平行四邊形(特別說來是作在半軸，上的長方形)面積之比值，因為有已知漸近線的所有雙曲線都同位相似，所以這個比值與半徑的取法無關.這時半徑所掃過的面積，因而也就是雙曲旋轉的角，按下列規則決定正負號.讓我們來討論那樣一對對頂角，它們是由第一條漸近線在繞著中心反時針方向直到與第二條漸近線重合的旋轉下所寫成的.在任意的具有已知漸近線的雙曲旋轉下,落在這一對對頂角里的點的半徑,或者都作反時針方向的旋轉,或者都順時針方向的旋轉.我們把這些半徑反時針方向所掃過的面積算作正的，順時針方向所掃過的面積算作負的.在另一對對頂角里所有的半徑向著相反的方向旋轉;那兒我們把順時針方向所掃過的面積算作正的，反時針方向所掃過的面積算作負的.總之,在一個雙曲旋轉下，如果落在第一對對頂角里的半徑反時針方向旋轉，則這個雙曲旋轉的角算作正的，否則算作負的。恆等的雙曲旋轉(也就是當作雙曲旋轉著的恆等變換)的角等於零。顯然，角為正的雙曲旋轉有係數τ>1，角為負的則有係數τ<1，反之亦然，雙曲旋轉的角可以採取-∞和+∞中間的任意實數值。

在前一段里我們看到過,雙曲旋轉的係數在變換誘發時保留著。證明實質上是根據這樣的事實：這個係數是兩個共線向量的比值，而共線向量的比值在仿射變換(它就是用來造成誘發的)下不變，然而在仿射變換下不變的還有面積的比值，因為雙曲旋轉的角定義作為兩個面積的比值，所以我們由此得到結論：雙曲旋轉的角在變換誘發時保留不變。