基本介紹
- 中文名:共軛雙曲線
- 外文名:conjugate hyperbola
- 所屬學科:數學
- 特點:有相同的漸近線等
- 相關概念:漸近線、雙曲線、焦點、離心率等
定義
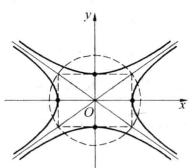 圖1
圖1相關性質定理



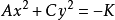
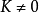









例題解析

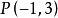
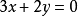





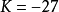


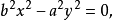
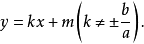

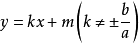



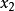


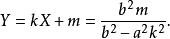
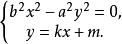

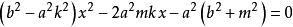

 圖2
圖2 圖3
圖3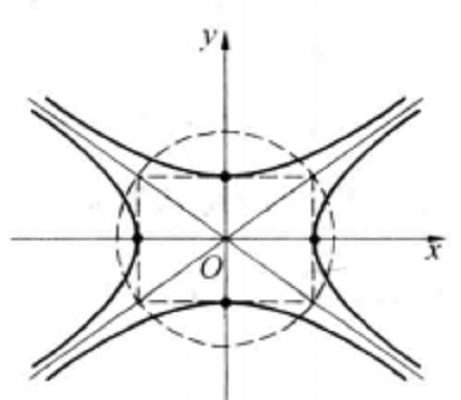
 圖1
圖1


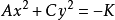
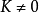










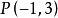
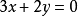





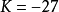


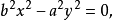
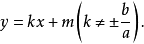

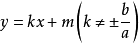





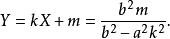
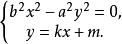

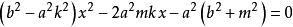

 圖2
圖2 圖3
圖3共軛雙曲線是兩條具有特殊位置的雙曲線,如果一雙曲線的實軸及虛軸分別為另一雙曲線的虛軸及實軸,則此二雙曲線互為共軛雙曲線。它們有相同的漸近線,並且4個焦點...
共軛即為按一定的規律相配的一對。通俗點說就是孿生。在數學中有共軛複數、共軛根式、共軛雙曲線、共軛矩陣等。中文名 共軛 外文名 Conjugate 類別 數學 基本...
漸近線定義為如果曲線上的一點沿著趨於無窮遠時,該點與某條直線的距離趨於零,則稱此條直線為曲線的漸近線。雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解決...
在R,對於非零的a,點集 是雙曲線。左邊和右邊的會經過a和 − a。a = 1稱為單位雙曲線。共軛雙曲線是 ,會分別經過ja和-ja。雙曲線和共軛雙曲線會被成...
雙曲旋轉(revolution of hyperbolic)是一種平面仿射變換,即將雙曲線繞其中心旋轉的平面仿射變換,在平面直角坐標系中,雙曲旋轉的計算公式為:x'=xchφ+y(a/b)sh...
實軸分為雙曲線中的實軸及複數平面中的實軸兩類。雙曲線中,雙曲線與坐標軸兩交點的連線段AB叫做實軸,長度為2a;複數域中,複數域與 x 軸上的點一一對應,把 ...
內接多邊形 內接五邊形 外切三角形 外切多邊形 共軛雙曲線斜二測畫法 三垂線定理 平行六面體 直接積分法 換元積分法第二積分法 分部積分法 混循環小數 第一積分...
一 證明曲線的幾何性質 1.證明曲線的焦半徑性質 2.證明曲線的焦點弦性質 3.證明曲線一般弦的性質 4.證明共焦點的二曲線性質 5.證明共軛雙曲線、等軸雙曲線性質...
6.等軸雙曲線與共軛雙曲線 7.拋物線及其標準方程 8.直線與圓錐曲線的位置關係 高頻考點 考點1圓錐曲線的定義 考點2圓錐曲線的方程 考點3橢圓和雙曲線的...
《淺談 由共軛雙曲線生活費確定雙曲線一類問題的教學》(安徽教育學院《中學數學教學》19 9 0年第6期)、《談套用複數運算幾何意義解題的教學》(安徽教育學院學院《...
雙曲線的焦點半徑 雙曲線的離心率 等軸雙曲線 共軛雙曲線 雙曲線的方程和性質 點與雙曲線的關係 直線與雙曲線的關係 雙曲線的切線公式 雙曲線切線的性質 雙曲線...
