基本介紹
- 中文名:雙曲線漸近線
- 範圍:|x|≥a,y∈R.
- 頂點:兩個頂點A1(-a,0),A2(a,0)
- 對稱性:雙曲線的對稱性與橢圓完全相同
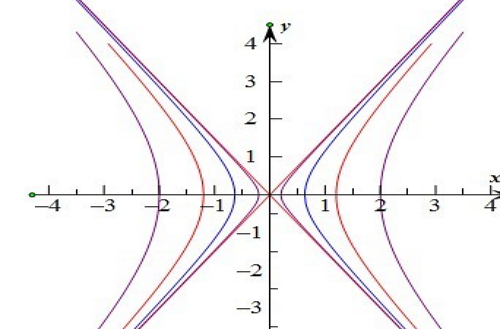
漸近線定義為如果曲線上的一點沿著趨於無窮遠時,該點與某條直線的距離趨於零,則稱此條直線為曲線的漸近線。雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解決...
雙曲線漸近線方程,是一種幾何圖形的算法,這種主要解決實際中建築物在建築的時候的一些數據的處理。漸近線的主要特點:無限接近,但不可以相交。分為鉛直漸近線、水平...
一般的,雙曲線(希臘語“ὑπερβολή”,字面意思是“超過”或“超出”)是定義為平面交截直角圓錐面的兩半的一類圓錐曲線。它還可以定義為與兩個固定的...
漸近線與雙曲線內容簡介 編輯 平淡不離奇,樸實不虛化;平凡的人演繹偉大的愛情;在青春洋溢的校園裡,溫文爾雅的纖纖少女江文撞上了兇狠殘暴的夏明,偶爾的碰撞下他們...
漸近線是指:曲線上一點M沿曲線無限遠離原點或無限接近間斷點時,如果M到一條直線的距離無限趨近於零,那么這條直線稱為這條曲線的漸近線。可分為垂直漸近線、水平...
王淵超於1995年讀高中時創作了這首歌曲。創作靈感來源於一堂解析幾何課,當時老師正在論證講解“雙曲線與漸近線只能無限接近不能達到”,而正是這點給王淵超帶來了創作...
實軸和虛軸等長的雙曲線叫做等邊雙曲線。此時,在雙曲線方程x^2/a^2-y^2/b^2=1中,a=b,於是得x^2-y^2=a^2。雙曲線的漸近線方程y=±(b/a)x變為y...
正雙曲線是指漸近線互相垂直的雙曲線,即半長軸與半短軸相等。也稱直角雙曲線。...... 正雙曲線是指漸近線互相垂直的雙曲線,即半長軸與半短軸相等。也稱直角雙...
雙曲面的漸近錐面(asymptotic conical surface of hyperboloid)是刻畫雙曲面形狀的錐面,由經過雙曲面中心的雙曲面的漸近線所組成的錐面。雙曲面族(x2/a2)+(y2/b2...
雙曲旋轉(revolution of hyperbolic)是一種平面仿射變換,即將雙曲線繞其中心旋轉的平面仿射變換,在平面直角坐標系中,雙曲旋轉的計算公式為:x'=xchφ+y(a/b)sh...
漸近線是指:曲線上一點M沿曲線無限遠離原點或無限接近間斷點時,如果M到一條直線的距離無限趨近於零,那么這條直線稱為這條曲線的漸近線。可分為垂直漸近線、水平...
