平面仿射坐標變換是一種坐標變換,指平面上任一點對於兩個仿射坐標系的坐標之間的對應關係。平面上點的仿射坐標變換公式和平面上向量的仿射坐標變換公式。
基本介紹
- 中文名:平面仿射坐標變換
- 外文名:Plane affine coordinate transformation
- 所屬學科:數學
- 所屬問題:空間解析幾何(坐標系)
基本介紹





平面仿射坐標系
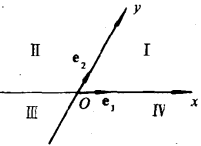
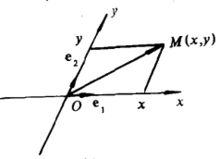
平面上點的仿射坐標





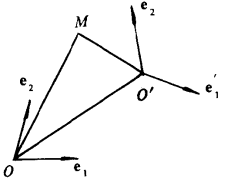
點的仿射坐標變換公式












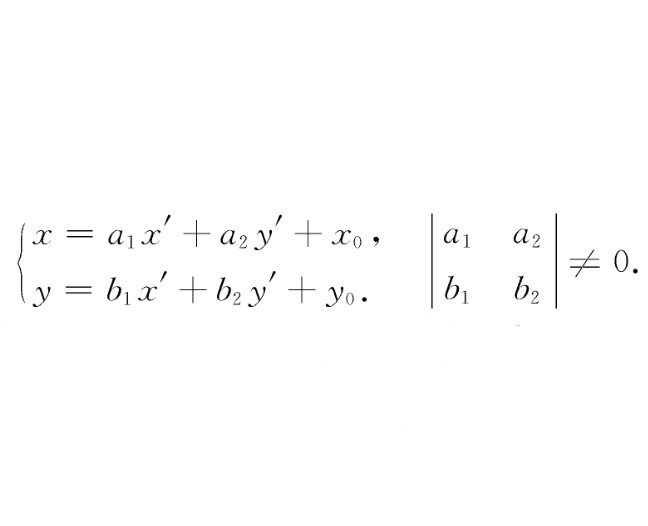
平面仿射坐標變換是一種坐標變換,指平面上任一點對於兩個仿射坐標系的坐標之間的對應關係。平面上點的仿射坐標變換公式和平面上向量的仿射坐標變換公式。

























平面仿射坐標變換是一種坐標變換,指平面上任一點對於兩個仿射坐標系的坐標之間的對應關係。平面上點的仿射坐標變換公式和平面上向量的仿射坐標變換公式。基本介紹設任一點M在仿射標架{O;e1,e2}中的坐標為(x,y),在仿射標...
平面仿射坐標(affine coordinates in plane)是一種平面坐標,平面上取兩條相交的軸x與y,交點O稱為原點,在兩軸上各取一個單位點E₁,E₂,使x軸和y軸都成為坐標軸,對於平面上的任意點M,過M作兩軸的平行線,設它們與軸x,y的交點分別為M₁,M₂,它們在軸x,y上的坐標分別為x,y,因而點M對應...
舉例而言,假如仿射變換於一平面上且假如A之行列式為1或-1,那么該變換即為等面積變換。此類變換組成一稱為等仿射群的子集。一同時為等面積變換與相似變換之變換,即為一平面上保持歐幾里德距離不變之保距映射。 這些群都有一保留了原定向的子群,也就是其對應之A的行列式大於零。在最後一例中,即為三維中剛體...
時稱為等積仿射變換。仿射變換的全體組成群,稱為仿射變換群。仿射變換最基本的性質是把任意共線的三點變換為共線的三點。相關分析 今有兩個相異或非相異平面[P]和[P’],其上面的點分別按坐標系XOY和X'O'Y'‘定位。這兩個平面上對應點之間的一一對應變換叫做單應變換或直射變換,它由以下齊次坐標關係式 ...
平面仿射幾何主要研究平面圖形在仿射變換下不改變的性質。仿射群 仿射群是由那些使矩陣為可逆矩陣的映射組成的平面的變換群。這樣的變換稱為仿射變換。仿射變換 仿射空間中最重要的變換是仿射變換,它的特徵是將共線的三點變為共線的三點。給定仿射坐標系後,仿射變換有明確的代數表示。仿射變換全體構成的變換群稱為...
中心仿射變換是指含一個不變點的仿射變換,這個不變點稱為中心仿射變換的中心。在以變換中心為坐標原點的仿射坐標系中,中心仿射變換公式右端的常數項為0。例如,在平面仿射坐標系中,變換 是一個中心仿射變換,其變換中心為坐標原點。在平面和空間的變換下,可以有—些點或圖形的象就是它們自己,這就是說它倆並...
笛卡爾坐標系(Cartesian Coordinates)就是直角坐標系和斜角坐標系的統稱。相交於原點的兩條數軸,構成了平面仿射坐標系。如兩條數軸上的度量單位相等,則稱此仿射坐標係為笛卡爾坐標系。兩條數軸互相垂直的笛卡爾坐標系,稱為笛卡爾直角坐標系,否則稱為笛卡爾斜角坐標系。相交於原點的三條不共面的數軸構成空間的仿射...
線性變換方法 射影坐標變換的解析表示是滿秩(非異)齊次線性變換。據此,可以得到射影坐標系的又一種建立方式。設在p(或擴大歐氏平面,或擴大仿射平面)上已建立了齊次坐標 ,令 則 是射影坐標。 這個坐標系的基點和麼點不難從變換方程求得。三線坐標 這是歐氏平面上非無窮遠點的射影坐標的度量解釋。設在歐氏...
橢圓旋轉(revolution of an ellipse)是一種平面仿射變換,即將橢圓繞其中心旋轉的平面仿射變換。在平面直角坐標系中,橢圓旋轉τ:(x,y)→(x′,y′)的計算公式為x′=x cos φ-y(a/b)sin φ,y′=x·(b/a)sin φ+ycos φ。基本介紹 平面上把橢圓變成自己的仿射變換用平面上把圓周變成自己的仿射變換...
雙曲旋轉(revolution of hyperbolic)是一種平面仿射變換,即將雙曲線繞其中心旋轉的平面仿射變換,在平面直角坐標系中,雙曲旋轉的計算公式為:x'=xchφ+y(a/b)shφ,y'=x(b/a)shφ+ychφ。雙曲旋轉的定義和總的描述 下面說明關於把雙曲線變成它自已的非常重要的平面仿射變換。取任意一對相交的...
3 直線的方程,直線、平面間的相關位置 習題1.3 4 點、直線和平面之間的度量關係 習題1.4 第三章 常見曲面 1 球面和旋轉面 習題1.1 2 柱面和錐面 習題1.2 3 二次曲面 習題1.3 4 直紋面 習題1.4 5 曲面的交線,曲面所圍成的區域 習題1.5 第四章 坐標變換 1 平面的仿射坐標變換 習題1.1 2 ...
§5 空間直角坐標變換 5.1 平移 5.2 旋轉 5.3 一般的坐標變換 §6 二次曲面的分類定理 問題與練習 第六章 變換群與幾何學 §1 變換群 1.1 點變換 1.2 變換群 §2 正交變換與歐氏幾何 2.1 基本概念 2.2 代數表示式 2.3 正交變換群 §3 仿射變換與仿射幾何 3.1 平面上的仿射坐標系與仿射變換...
