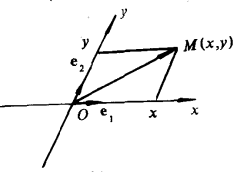
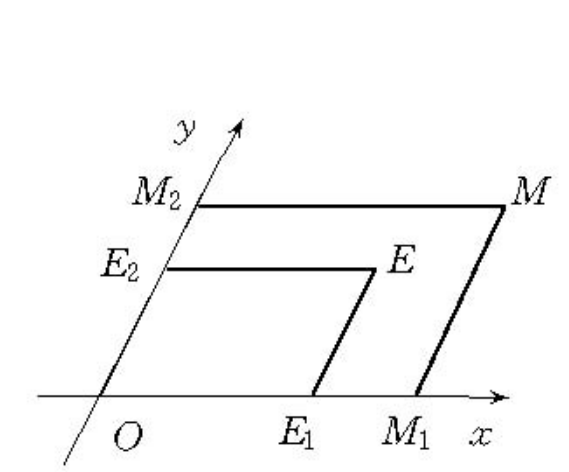
平面仿射坐標(affine coordinates in plane)是一種平面坐標，平面上取兩條相交的軸x與y，交點O稱為原點，在兩軸上各取一個單位點E1，E2，使x軸和y軸都成為坐標軸，對於平面上的任意點M，過M作兩軸的平行線，設它們與軸x，y的交點分別為M1，M2，它們在軸x，y上的坐標分別為x，y，因而點M對應著有序實數對(x，y)，反過來，任意給一有序實數對(x，y)，可以分別在x，y軸上作出坐標為x，y的點M1，M2，過M1，M2分別作y軸、x軸的平行線，得到其交點M，可見平面上所有點與全體有序實數對(x，y)之間存在一一對應關係，這個一一對應關係稱為平面仿射坐標系，又稱平行坐標系，有序實數對(x，y)稱為點M的平面仿射坐標，x，y分別稱為點M的第一坐標和第二坐標。平面仿射坐標系的兩軸上，長度單位一般不同，如果相同就是斜坐標系，兩軸的夾角可為任意角，若等於直角，且兩軸上的長度單位相同，則為直角坐標系。
基本介紹
- 中文名：平面仿射坐標
- 外文名：affine coordinates in plane
- 所屬學科：數學
- 所屬問題：平面解析幾何
- 簡介：一種平面坐標
平面仿射坐標系,平面上點的仿射坐標,
平面仿射坐標系
在平面解析幾何中，通過在平面上建立直角坐標系或極坐標系，把平面上的點與一對有次序的數對應起來，把平面上的圖形與二元方程對應起來，從而用代數方法來研究平面幾何問題。需要指出的是，建立平面上的點與一對有次序的數之間的對應關係並不限於直角坐標系或極坐標系。還有另一種更為一般的坐標系——仿射坐標系。
在平面上取定一點O和兩個以點O為起點的不共線向量e1，e2，稱為平面上的一個仿射坐標系，記作{0；e1，e2}。其中O稱為原點，e1，e2稱為基向量(簡稱基)或坐標向量。若e1，e2符合右手規則，則稱此坐標係為右手系，否則稱為左手系。如不特別聲明，一般指右手系。過O點且分別平行於e1，e2的有向直線(它的正向與基向量的方向相同)稱為坐標軸。共有兩條坐標軸，依次稱為x軸和Y軸。兩條坐標軸分平面為四部分，依次稱為第Ⅰ，Ⅱ，Ⅲ，Ⅳ象限(如圖1所示)。
圖1
若仿射坐標系{0；e1，e2}的基向量e1，e2互相垂直，且|e1|=|e2|=1，就成為平面直角坐標系。可見，平面直角坐標系是平面仿射坐標系的特殊情形。
平面上點的仿射坐標
在平面仿射坐標系{0；e1，e2}中給定一點M，就確定唯一的向量
，稱為點M的向徑。向徑 可唯一地表示成
如圖2所示。由此可見，向徑 與有序數組(x，y)之間建立了一一對應關係。有序數組(x，y)稱為向徑 在仿射坐標系{0；e1，e2}下的坐標，也稱為點M在仿射坐標系{0；e1，e2}下的坐標，記作M(x，y}。
圖2
