基本介紹
- 中文名:交角公式
- 所屬學科:數學
- 所屬問題:向量和三角函式
- 相關概念:餘弦定理,兩向量的夾角
基本介紹









相關介紹
兩向量的夾角






內積的性質




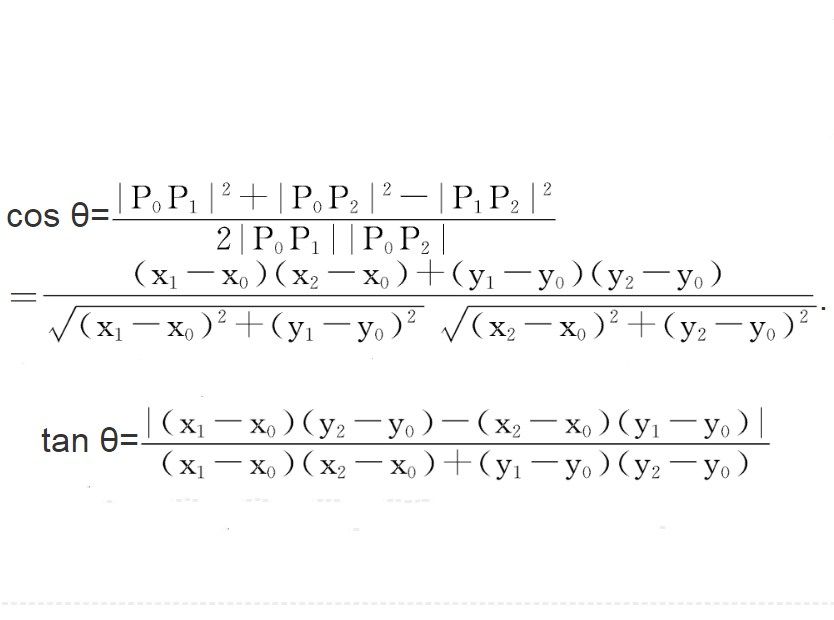



















交角公式是計算角的一種公式,設點Pi的直角坐標為(xi,yi)(i=0,1,2),則以射線P0P1與P0P2為邊的角θ∈(0,π)可由余弦定理而得。可以從兩向量的夾角思考交角公式。基本介紹交角公式的依據——餘弦定理 餘弦...
黃赤交角,天文學術語,是指在地心天球上,地球公轉軌道面(黃道面)與赤道面(天赤道面)的交角,又名黃道交角、黃赤大距。其中,黃道與天赤道的兩個交點,叫牡羊宮(牡羊座)第一點和天秤宮(天秤座)第一點,在北半球分別稱為...
拉蓋爾定理(Laguerre theorem)是射影幾何的重要定理之一。設兩條非迷向直線的交角為θ,若這兩條直線與過它們交點的兩條以-i,i為斜率的迷向直線所成的交比為μ,則θ=(ln μ)/2i,由拉蓋爾定理可得到:兩條非迷向直線垂直的...
正切公式 設直線 、的斜率存在,分別為 、,與 的夾角為 ,則 。注意:兩直線的夾角指的是兩直線所成的小於等於90°的角,但是當夾角為90°時,k不存在,故當k存在時,正切值始終為正。餘弦公式 A1X+B1Y+C1=0...(1)A2X+B...
“到角”是帶有方向的角,故叫有向角。公式的分子部分是逆時針方向箭頭所指的直線斜率減去另一斜率,與夾角公式不同。與到角相類似的夾角是只是大小,只是兩角之差的絕對值。套用 套用於求對稱直線的斜率。已知直線 的斜率為 ,又...
可以通過斜率來判斷兩條直線是否互相平行或互相垂直,也可計算它們的交角。直線與某個坐標軸的交點在該坐標軸上的坐標,稱為直線在該坐標軸上的截距。直線在平面上的位置,由它的斜率和一個截距完全確定。在空間,兩個平面相交時,交線...
運用該公式也可以求異面直線所成角。向量法 向量幾何法。運用向量的加減法規則,把要求的異面直線用向量表示,並運用向量的運算法則(例如分配律、共線向量)來求出cosθ 向量代數法。當容易找到三條兩兩垂直的直線時,可以以它們的...
圖1中PA 是一個球面,球心為O,半徑為r。光軸為AOBC。入射光線在P點與球面相交,入射線與球面的垂直線交角為i1,入射線的延長線與光軸相交於C,交角為U1;折射線與光軸相交於B點,交角為U2。AC=L1,AB=L2。在球面左邊介質的...
§14.交角公式 §15.面積 第三章曲線及方程式 §16.曲線之方程式 §17.方程式之軌跡 §18.方程之討論 §19.撮要 §20.水平及垂直漸近線 §21.交點 第四章直線 §22.任何直線方程之次數 §23.任何一次方程之軌跡 §24....
也就是說,地球在公轉過程中地軸是平行地移動的,所以無論地球公轉到什麼位置,地軸與地球軌道面的夾角是不變的,黃赤交角是不變的。黃赤交角的存在,也表明黃極與天極的偏離,即黃北極(或黃南極)與天北極(或天南極)在天球上...
直角標架分別是{O;t, j}和{}r; it }}r,而且藝C1,1O=B,即x軸和x'軸的交角是B.於是i'=cosBi}-sing j, j'_ -sin Bi -}cos方.再設新坐標原點O'的舊坐標為}xo,yo}.直角坐標變換的公式是 ...
黃道與赤道之間的夾角,即地球軌道平面(即黃道平面)與赤道平面之間的交角,稱黃赤交角。當今世界上公認的黃赤交角度數為23°26′21″,是1976年在國際天文學聯合會第十六屆大會上根據1901年紐康提出的計算黃赤交角的公式,參考標準...
公式推導 1808年,馬呂斯經實驗指出,強度為I₀的線偏振光,透過檢偏片後,透射光的強度(不考慮吸收)為:I=I₀cos² α 其中, α是入射線偏振光的光振動方向和偏振片偏振化方向之間的夾角.一束光強為I₀的線偏振光,透過檢偏器...
c(cosγ-cosγ0)=lλ式中,b、c為晶胞邊長;0、β0、γ0是入射線與晶胞基向量的夾角;、β、γ是衍射線與晶胞基向量的夾角;h、k、l是三個正整數,稱為衍射指數;λ是X射線的波長。布拉格方程 描述X射線衍射條件,還可以...
(2)如果小區的規劃區面積足夠大,可以考慮降低樓層(多蓋幾幢)、拉大樓距的辦法;如果小區的規劃區面積不允許,則可以採用錯落有致的辦法來布局。同時,也可以考慮把住宅樓的走向定為與子午線成30°~60°夾角的走向。
常用公式 1、求函式圖像的k值:(y₁-y₂)/(x₁-x₂),即k=tanα(α為直線與x軸正方向的夾角)2、求與x軸平行線段的中點:(x₁+x₂)/2 3、求與y軸平行線段的中點:(y₁+y₂)/2 4、求任意線段的...
公式 毛細現象中液體上升下降的高度可由下式確定:式中,r為細管半徑;ρ為液體密度;θ為液面與管壁的交角,它取決於液、氣種類和管壁材料等因素,對於水和潔淨的玻璃θ=0°,水銀和玻璃θ=140°。生物現象 1、根和莖的毛細現象...
6.1 兩直線的交角 6.2 兩平面的交角 6.3 直線與平面的交角 6.4 點到直線的距離 6.5 兩直線間的距離 6.6 點到平面的距離 §7 平面束 §8 例 結束語 問題與練習 第四章 幾種常見的曲面和曲線 §1 圖形與方程 1.1 ...
在數學中,極坐標系是一個二維坐標系統。該坐標系統中任意位置可由一個夾角和一段相對原點—極點的距離來表示。極坐標系的套用領域十分廣泛,包括數學、物理、工程、航海、航空以及機器人領域。在兩點間的關係用夾角和距離很容易表示時,...
角平分線定理1是描述角平分線上的點到角兩邊距離定量關係的定理,也可看作是角平分線的性質。角平分線定理2是將角平分線放到三角形中研究得出的線段等比例關係的定理,由它以及相關公式還可以推導出三角形內角平分線長與各線段間的定量...
6.1 兩直線的交角 6.2 兩平面的交角 6.3 直線與平面的交角 6.4 點到直線的距離 6.5 兩直線間的距離 6.6 點到平面的距離 7 平面束 8 例 結束語 問題與練習 第四章 幾種常見的曲面和曲線 1 圖形與方程 1.1 曲面與...
按照直線與平面所成角的定義。一般通過面的垂線,確定斜線射影。轉化成斜線與射影的夾角。然後,解三角形求角。(2)法向量法 1°轉化成平面的法向量,與斜線的方向向量所成角的餘角,或補角的餘角。即用公式 sin=|n·b|/|n||b...
天文緯度(astronomical latitude)是地球上的緯度的一種,地面上的點在大地水準面上的緯度,即在所在地的鉛垂線(大地水準面法線)同地球赤道平面的交角。它等於天極的高度,也等於天頂的赤緯。通過對天體的觀測進行測定,受局部地區的鉛垂直...
