晶體X射線衍射

晶體X射線衍射是X射線在晶體中發生的衍射現象。晶體具有點陣結構，點陣結構的周期（即晶胞邊長，b，c）與X射線 的波長屬於同一數量級，X射線衍射現象是一種基於波疊加原理的干涉現象，干涉的結果隨不同而有所不同（Δ為波程差；λ為波長）。

X射線為整數的方向，波的振幅得到最大程度的加強，稱為衍射，對應的方 向為衍射方向 ，而為半整數的方向，波的振幅得到最大程度的抵消。因此，X射線通過晶體之後，在某些方向（衍射方向）X射線的強度增強，而另一些方向X射線強度卻減弱甚至消失 ，如果在晶體的背後放置一張感光底片，將會得到X射線的衍射圖形。

基本介紹

• 中文名：晶體X射線衍射
• 外文名：X-ray diffrection by crystals
• 類別：衍射現象
• 計算公式：布拉格方程

晶格參數

利用X射線衍射原理製造的X射線衍射儀，是測定晶體結構的最主要儀器。根據衍射的方向可以測定晶 格參數或晶胞的大小和形狀。根據衍射線強度分布能夠測定原子在晶胞中的坐標，因此X射線衍射法也是測定分子空間構型的主要方法。

晶體X射線衍射

產生晶體X射線衍射的條件可用勞厄方程來描述，勞厄方程的標量表達式如下：

（cos－cos0）=hλ

b（cosβ－cosβ0）=kλ

c（cosγ－cosγ0）=lλ式中，b、c為晶胞邊長；0、β0、γ0是入射線與晶胞基向量的夾角；、β、γ是衍射線與晶胞基向量的夾角；h、k、l是三個正整數，稱為衍射指數；λ是X射線的波長。

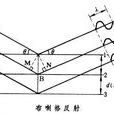
布拉格方程

描述X射線衍射條件，還可以用布拉格方程：

X射線衍射的基本原理

2dsinθ=nλ式中d為相鄰兩個晶面之間的距離；θ為入射線或反射線與晶面的交角；λ為X射線波長；n 為正整數。布拉格方程與勞厄方程雖然表達方式不同，但其實質是相同的。

當 X射線的波長與入射線方向以及晶體方位確定以後，勞厄方程中的λ、、b、c、0、β0、γ0 都已確定，只有、β、γ是變數，它們必須滿足勞厄方程，但是，、β、γ3個變數不是獨立的，例如在直角坐標中應滿足：

cos2+cos2β+cos2γ=1這就是說，3個變數、β、γ應同時滿足4個方程，這在一般條件下是不可能的，因而得不到衍射圖。為了解決這個問題，必須再增加一個變數，有兩種辦法可供選擇：①晶體不動（0、β0、γ0固定），改變波長λ，即採用白色X射線，這種方法稱為勞厄法；②波長不變，即用單色X射線 ，讓晶體繞某晶軸轉動，即改變0、β0、γ0 。這樣可在某些特定的晶體方位得到衍射圖，這種方法叫做轉動晶體法。以上兩種方法都是對單晶體而言的。如果晶體是多晶，每個小單晶體在空間的取向是隨機的，勞厄方程總可以得到滿足，這就是粉末法的基礎。

發現歷程

德國物理學家 M.von勞厄於1912年發現上述現象，他構想，如能找到一種波長為 10-8納米的電磁波， 讓它通過晶體，必能發生衍射現象，能提供晶體內原子排布的信息。那時曾有些人為驗證 X射線是電磁波而採用普通光柵作衍射實驗而屢遭失敗。由此勞厄想到,X射線是一種波長比可見光短得多的電磁波，它可能是晶體衍射的合適射線。通過實驗，勞埃和助手們證實了他們的構想，他因此獲得1914年的諾貝爾物理學獎。

晶體X射線衍射